เฉลยข้อ 3 (เรียบเรียงตามหนังสือ)
ถ้ามีป้าย 2 ป้าย P กับ Q จาก (2) บอกว่าจะมีอย่างน้อย 1 สายที่ผ่านสองป้ายนั้น แต่ถ้าสมมติว่ามีมากกว่า 1 สายผ่าน 2 ป้ายนั้นมันจะเกิดข้อขัดแย้งกับ (3) เพราะนั่นคือมีสายรถมากกว่า 1 สายที่แชร์ป้ายร่วมกัน 2 ป้าย ฉะนั้นเราได้ กฎเพิ่มขึ้นมาอีกข้อครับ
(4) สำหรับสองป้ายใด ๆ P กับ Q จะมีสายรถเพียงสายเดียวเท่านั้นที่เชื่อมระหว่างมัน
ถ้าให้ f(P) แทนจำนวนสายรถที่ผ่านป้าย P และให้ g(l) แทนจำนวนป้ายของสาย l อันดับแรกเราจะพิสูจน์ว่า (5) ถ้า P ไม่อยู่บน l แล้ว f(P) = g(l)
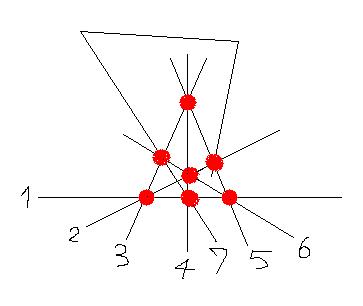
ตรงนี้ลองวาดรูปครับ เส้น l ที่มี g ป้าย คือป้ายที่ 1, 2, 3, ..., g หรือ g(l) = g แล้วก็วาดจุด P ที่ไม่อยู่บน l เนื่องจากจุด P แตกต่างกับทุก ๆ ป้ายบน l จาก (4) จึงทำให้มี f(P) = g นั่นคือ f(P) = g(l)
จากนั้นพิจารณาสาย 2 สาย a กับ b (ลองวาดรูปนะครับ) เราจะพิสูจน์ว่า (6) มีป้ายรถ P ที่ไม่ได้อยู่บนทั้งสาย a และ b
จาก (3) a และ b มีป้ายร่วมคือ C, จาก (1) a มีอย่างน้อย 3 ป้าย ดังนั้นต้องมีป้าย A ที่ไม่ใช่ C อยู่บน a ทำนองเดียวกันต้องมีป้าย B ที่ไม่ใช่ C อยู่บน b และจาก (4) จะต้องมีสายรถที่ผ่าน A-B ซึ่งบนสายนี้จะต้องมีอย่างน้อยอีก 1 ป้าย (จาก (1)) และป้ายนั้นคือ P ซึ่ง P นี้ไม่อาจอยู่ได้ทั้งบน a และ b เพราะจะทำให้เกิดการฝ่าฝืนกับ (3)
จาก (5) เราได้ว่า g(a) = f(P) และ g(b) = f(P) เพราะฉะนั้น g(a) = g(b) นั่นคือทุกสายเดินรถมีจำนวนป้ายหยุดรถเท่ากัน (จบพิสูจน์ 1.) และกำหนดให้จำนวนนั้นเท่ากับ n+1
ต่อมาเราต้องการพิสูจน์ว่า ถ้า P เป็นป้ายใด ๆ แล้ว f(P) = n+1 ด้วย ซึ่งก็ไม่ยากเย็นอะไรครับ เพราะเราแค่เพียงพิสูจน์ว่ามีสายบางสาย l ที่ไม่ผ่าน P ก็พอแล้วที่จะทำให้ f(P) = g(l) = n+1 ก็เริ่มจากเลือกป้ายรถสองป้าย P และ Q ที่แตกต่างกัน มันก็ต้องมีสาย d ที่เชื่อมระหว่างสองป้ายนั้น จากข้อกำหนดของโจทย์เลยว่ามันจะต้องมีอย่างน้อย 2 สาย ฉะนั้นมันต้องมีป้าย R อีกป้ายที่ไม่อยู่บน d เราก็จะได้สาย l คือสายที่เชื่อม Q กับ R (จบพิสูจน์ 2.)
ต่อไปจะพิสูจน์จำนวนสายและป้ายรถบัสรวม
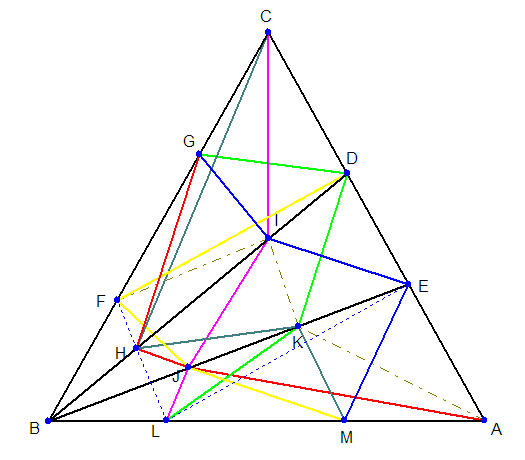
เลือกสาย l กำหนดให้มี n+1 ป้าย คือป้ายที่ 1, 2, 3, ..., n+1 สายอื่นที่ไม่ใช่สาย l จะมีป้ายร่วมกับ l หนึ่งป้าย และจากพิสูจน์ 2. เรารู้ว่าแต่ละป้ายมีรถผ่าน n+1 สาย (สาย l เป็นหนึ่งในนั้นด้วยนะครับ) ฉะนั้นมีสายรถทั้งหมด (n+1)n + 1 = n2 + n + 1 สาย (จบพิสูจน์ 3.)
เลือกป้ายรถ P เรารู้ว่ามีสายรถที่ผ่าน n+1 สายคือ 1, 2, 3, ... n+1 เรารู้ว่าทุก ๆ ป้ายจะต้องมีสายเชื่อมกับ P (จาก (4)) ซึ่งคำว่าทุก ๆ ป้ายนี้ แต่ละป้ายก็ต้องอยู่บนสายใดสายหนึ่งใน n+1 สาย เช่นสายที่ 1 มี n+1 ป้าย (ป้าย P เป็นหนึ่งในนั้นด้วยนะครับ) นั่นคือแต่ละสายมี n ป้ายที่ไม่ใช่ป้าย P ฉะนั้นมีจำนวนป้ายทั้งหมด n(n+1) + 1 ป้าย (จบพิสูจน์ 4.)
| จากคุณ |
:
ศล   
|
| เขียนเมื่อ |
:
11 ก.ค. 52 12:40:09
|
|
|
|
|
|