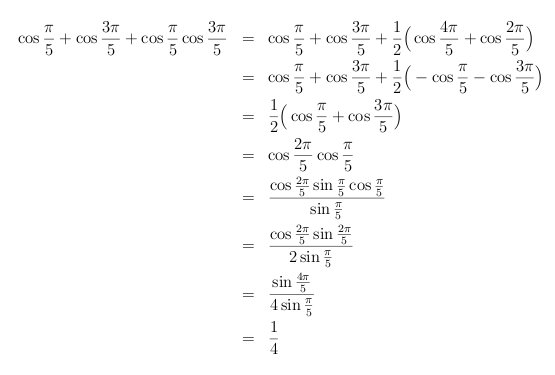 |
ความคิดเห็นที่ 21 |
 |
ตามติดความเห็น #13 ขอข้ามไปข้อ 4 ครับ
(ใช้ความรู้ complex number นิดหน่อย)
พิจารณาสมการ z^7 + 1 = 0
ซึ่งคือสมการ z^7 = -1 = cos(pi) + isin(pi)
สมการนี้มีรากคือ
cos(pi/7) + isin(pi/7), cos(3pi/7) + isin(3pi/7),
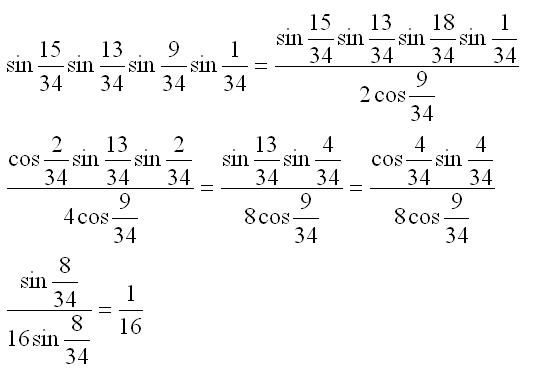
cos(5pi/7) + isin(5pi/7),cos(7pi/7) + isin(7pi/7) = -1,
cos(9pi/7) + isin(9pi/7), cos(11pi/7) + isin(11pi/7)
และ cos(13pi/7) + isin(13pi/7)
จากสมการ เราทราบว่าผลบวกของรากคือ 0
ดังนั้นผลบวกของส่วนจริงของรากทั้งหมดคือ 0 ด้วย
จึงได้ว่า
cos(pi/7) + cos(3pi/7) + cos(5pi/7) -1 + cos(9pi/7) + cos(11pi/7) + cos(13pi/7) = 0
cos(pi/7) + cos(3pi/7) + cos(5pi/7) + cos(9pi/7) + cos(11pi/7) + cos(13pi/7) = 1
แต่ cos(pi/7) = cos(13pi/7), cos(3pi/7) = cos(11pi/7) และ cos(5pi/7) = cos(9pi/7)
ดังนั้น
2[cos(pi/7) + cos(3pi/7) + cos(5pi/7) ] = 1
cos(pi/7) + cos(3pi/7) + cos(5pi/7) = 1/2
-----------------------------------------------------------------------------
ป.ล. ข้อนี้แทบจะเหมือนกับข้อสอบ IMO ปี 1963 ข้อ 5 ครับ :)
| จากคุณ |
:
Infinitum
|
| เขียนเมื่อ |
:
26 ก.ค. 52 11:51:35
A:218.186.178.161 X:218.186.10.234
|
|
|
|
|
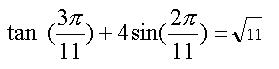
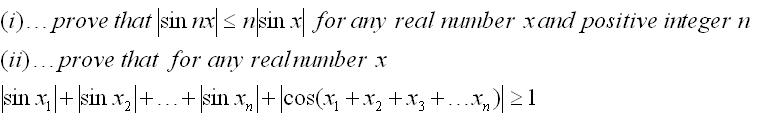
... เข้ามาดู
