|
 มีอะไรผิดตรงไหนครับ
มีอะไรผิดตรงไหนครับ

|
|
เจอโจทย์หลอกเด็กง่าย ๆ ที่มีแง่มุมอื่นที่ไม่ใช่คณิตศาสตร์-ไม่ใช่เรขาคณิตที่น่าสนใจเอามาฝากครับ
"You are allowed to lie a little, but you shold never mislead."
Paul R. Halmos นักคณิตศาสตร์ฮังกาเรียน-อเมริกัน
ประเด็นที่น่าสนใจของข้อนี้ ผมว่าอยู่ที่ 'lie' กับ 'mislead'
-------------------------------------------------------------------------------------------------------------
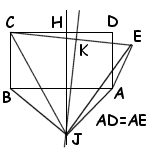
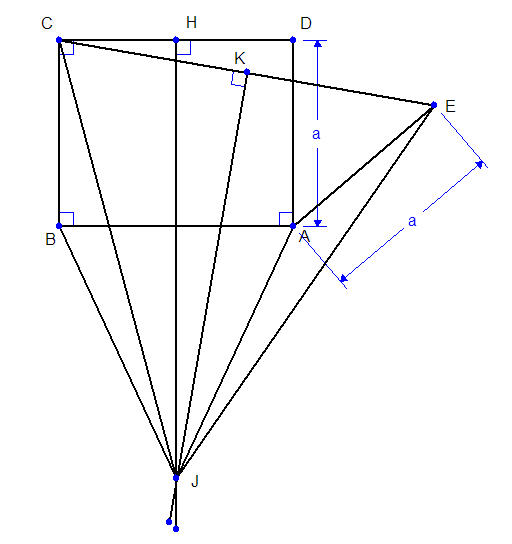
ในรูปด้านล่างนะครับ ABCD เป็นสี่เหลี่ยมผืนผ้า
E เป็นจุดที่อยู่ใกล้ D นอกสี่เหลี่ยมเล็กน้อยที่ทำให้ AE = AD
H เป็นจุดกึ่งกลางของ CD
K เป็นจุดกึ่งกลางของ CE
เส้นตรงที่ตั้งฉากกับ CD ลากผ่าน H
เส้นตรงที่ตั้งฉากกับ CE ลากผ่าน K
ทั้งสองเส้นตัดกันที่ J
คราวนี้เราลองมาพิจารณาด้านของสามเหลี่ยม BCJ กับ AEJ
1. BC = AE
(เพราะทั้งคู่นี้เท่ากับ AD)
2. JB = JA
(เพราะ J อยู่บนเส้นตรงที่ตั้งฉากกับ CD และแบ่ง CD ออกเป็นสองส่วนเท่า ๆ กัน มันก็ต้องแบ่ง AB ด้วย)
3. CJ = EJ
(เพราะ J อยู่บนเส้นตรงที่ตั้งฉากที่แบ่ง CE ออกเป็นสองส่วนเท่า ๆ กัน - ตามโจทย์)
แบบนี้เราก็สรุปได้ว่าสามเหลี่ยม BCJ กับ AEJ เป็นสามเหลี่ยมเหมือน (congruent triangle) ได้นะสิ
เพราะสามเหลี่ยมสองรูปนี้มีด้านเท่ากันทั้งสามด้าน
มุม JBA เท่ากับมุม JAB (เพราะสามเหลี่ยม JAB เป็นสามเหลี่ยมหน้าจั่ว)
จากรูปเห็นได้ชัดว่ามุม CBJ - มุม JBA ได้มุม ABC ซึ่งเป็นมุมฉาก
และมุม JAE - มุม JAB ได้มุม BAE ซึ่งเป็นมุมป้าน !!! เป็นไปได้ยังไง ?!?
มีอะไรผิดตรงไหนครับ?
| จากคุณ |
:
ศล   
|
| เขียนเมื่อ |
:
28 ก.ค. 52 16:26:38
|
|
|
|  |