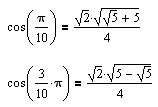|
 ความคิดเห็นที่ 17
ความคิดเห็นที่ 17 |

โอเคครับ คุณศล สมบูรณ์แล้วครับ 
สำหรับการแก้โจทย์ข้อนี้ก็ต้องให้เครดิตคุณศล, คุณ freefeel, และคุณ mint_la
ที่ช่วยกันทำคนละไม้คนละมือ มากบ้างน้อยบ้าง ขอบคุณทุกท่านนะครับ
อ้อ! ขอบคุณรูปจากคุณ nonlocality ด้วยครับ
-----------------------------------------------------------------------------------------------------------------
คราวนี้ขอเฉลยวิธีของ จขกท. บ้างครับ
ของผมไม่อาศัยการหาค่าทางตรีโกณฯ แต่ใช้ความรู้จำนวนเชิงซ้อน (ม.ปลาย) นิดหน่อยครับ
พิจารณาสมการ z^5 - 5^5 = 0
(z - 5)(z^4 + 5z^3 + 25z^2 + 125z + 625) = 0
(z - 5)(z - z1)(z - z2)(z - z3)(z - z4) = 0
โดยที่ 5, z1, z2, z3, z4 คือคำตอบทั้งห้าของสมการดังกล่าว
สังเกตว่า (z - z1)(z - z2)(z - z3)(z - z4) = z^4 + 5z^3 + 25z^2 + 125z + 625 ....... (*)
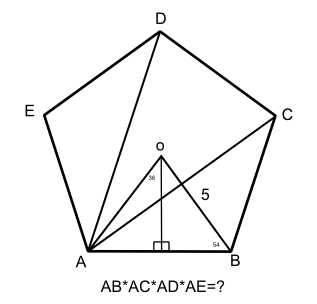
ให้จุด A = 5, B = z1, C = z2, D = z3, E = z4
ในระนาบเชิงซ้อน จุดทั้งห้าจุด จะเป็นจุดยอดของรูปห้าเหลี่ยมด้านเท่ามุมเท่า เพราะคือรากที่ห้าของ 5^5
และมี AO = 5 ตามที่โจทย์กำหนด ดังนั้นจะเห็นว่าค่าที่โจทย์ต้องการคือ
(AB)(AC)(AD)(AE)
= |(5 - z1)(5 - z2)(5 - z3)(5 - z4)|
= 5^4 + 5^4 + 5^4 + 5^4 + 5^4 [จาก (*)]
= 5^5 = 3125 
แก้ไขเมื่อ 30 ก.ค. 52 23:37:43
| จากคุณ |
:
Accenda 
|
| เขียนเมื่อ |
:
30 ก.ค. 52 23:36:20
|
|
|
|
 |