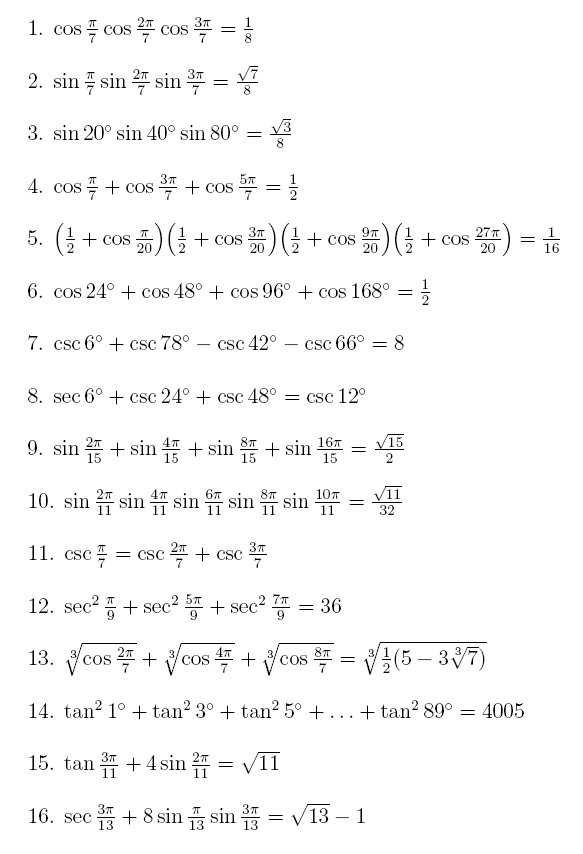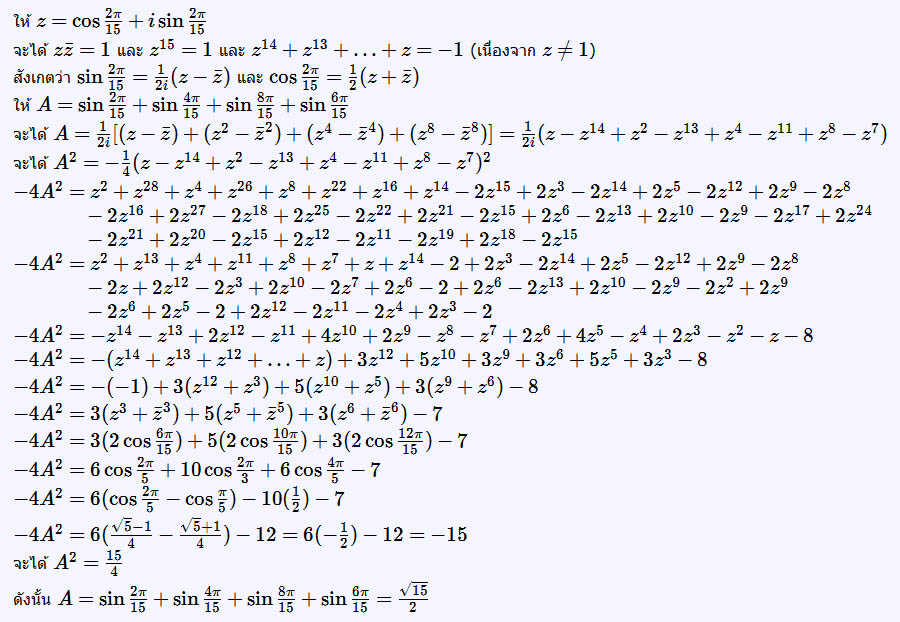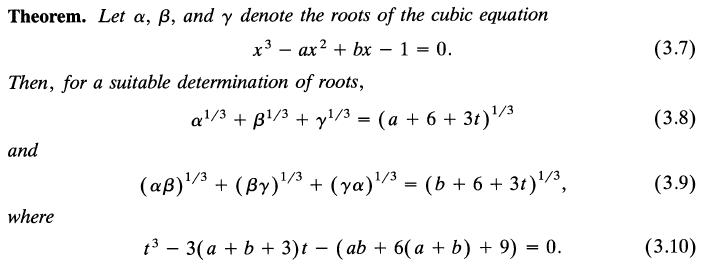|
 ความคิดเห็นที่ 36
ความคิดเห็นที่ 36 |

เห็นคุณ ZOHAN บอกว่า ข้อ 13 เป็นเอกลักษณ์ที่ Ramanujan
ก็เลยลองค้นโดย google ดู ปรากฎว่าเจอลิงค์นี้ (เป็นไฟล์ .PDF ครับ)
http://mathdl.maa.org/images/upload_library/22/Ford/Berndt-Bhargava644-656.pdf
ประเด็นหลักอยู่ที่หน้า 9-10 ครับ
ลองอ่านดูคร่าวๆ ก็รู้ว่าข้อ 13 ไม่ใช่ เอกลักษณ์ที่ Ramanujan พิสูจน์ เพียงแต่ว่าคล้ายคลึงกันมาก
แอบสงสัยว่า คงใช้หลักการแบบเดียวกัน แล้วประยุกต์ตัวเลขนิดหน่อยในการสร้าง
***มีการใช้สัญลักษณ์ทางคณิตศาสตร์ โปรดใช้ IE เปิดดู
สำหรับท่านผู้ใช้ Firefox ให้ติดตั้ง IE Tab***
ถ้าเราดูหน้า 9 จะเห็นว่าทฎษฏีของ Ramanujan นั้นใช้ x3-ax2+bx-1=0
แต่สำหรับข้อ 13 นั้นมี cos2p/7, cos4p/7, cos8p/7 มาเกี่ยวข้อง
และจากลิงค์ของคุณ ZOHAN ( http://www.mathcenter.net/sermpra/sermpra32/sermpra32p01.shtml )
ในหน้าแรกนั้น ทำให้เรารู้ว่า
รากของสมการ 8x3+4x2-4x-1=0 นั้นมี 3 ตัวคือ
x=cos2p/7, cos4p/7, cos8p/7
ทำให้เราต้องประยุกต์ทฤษฏีของ Ramanujan นิดหน่อย คือให้อยู่ในรูป 8x3-ax2+bx-1=0
เริ่มการประยุกต์
ให้สมการ 8x3-ax2+bx-1=0 ..........(*)
มีราก 3 ตัว คือ x1, x2, x 3
จัดรูปสมการเป็น x3-(a/8)x2+(b/8)x = 1/8
จากสมการจะเห็นได้อย่างชัดเจนว่า x1*x2*x3 =1/8
ต่อมาสมมุติ y1=x11/3, y2=x21/3, y3=x31/3
จะได้ว่า y1*y2*y3=(x1*x2*x3)1/3 = (1/8)1/3 = 1/2
ทำให้ทราบว่า y1, y2, y3 นั้น เป็นรากของสมการ 2y3-py2+qy-1 = 0 .........(**)
ต่อมา ยกกำลังสามสมการ (**) ทั้งสองข้างจะได้ว่า (2y3-1)3 = (py2-qy)3 จัดรูปให้สวยงามจะได้ว่า 8x3-(12+p3-6pq)x2+(6+q3-3pq)x-1=0 ............(***)
เอาสมการ (*) กับสมการ(***) มาเทียบกันจะเห็นได้ว่า
a=12+p3-6pq
b=6+q3-3pq
คูณ 2 ไปใน b ทั้งสมการได้ 2b = 12+2q3-6pq
ต่อมากำหนดให้ t=pq-6 แล้วเอาค่า t ไปแทนในสมการของ a และ b
จะได้ว่า
p3=a+24+6t
q3=b+12+3t
ส่วน t=pq-6 นั้นย้ายข้างได้ pq=t+6
จับ pq=t+6 ยกกำลังสามทั้ง 2 ข้างได้
(pq)3=(a+24+6t)(b+12+3t)=(t+6)3
จัดรูปให้สวยงามจะได้ว่า
t3-3(a+2b+12)t-{ab+12(a+2b+6)}=0
จับสมการ (**) 2y3-py2+qy-1 = 0 มาจัดรูปได้
y3-(p/2)y2+(q/2)y-(1/2) = 0
จากทฤษฎีสมการจากลิงค์ของคุณ ZOHAN ทำให้เราทราบทันทีว่า
y1+y2+y3=p/2
x11/3+x21/3+x31/3=(a+24+6t)1/3/2
กับ
y1y2+y2y3+y3y1=q/2
(x1x2)1/3+(x2x3)1/3+(x3x1)1/3=(b+12+3t)1/3/2
________________________________________________
สรุปการประยุกต์ทฤษฏีของ Ramanujan ที่ทำมาทั้งหมดได้ว่า
สมการ 8x3-ax2+bx-1=0 มีรากเป็น x1, x2, x3 แล้ว
x11/3+x21/3+x31/3=(a+24+6t)1/3/2
กับ
(x1x2)1/3+(x2x3)1/3+(x3x1)1/3=(b+12+3t)1/3/2
โดย t3-3(a+2b+12)t-{ab+12(a+2b+6)}=0
_________________________________________________
กลับมาเข้าสู่โจทย์ข้างต้นที่ผมกล่าวไว้ นั่นคือ 8x3+4x2-4x-1=0
จะเห็นว่า a=-4,b=-4 และ x1=cos2p/7, x2=cos4p/7, x=cos8p/7
เอาไปแทนในทฤษฎี Ramanujan ที่ถูกประยุกต์ด้านบน จะได้ว่า
t3=-56
t=-2(7)1/3
เอาค่าเหล่านี้ไปแทนได้
(cos2p/7)1/3+(cos4p/7)1/3+(cos8p/7)1/3={(1/2)*(5-3*(7)1/3}1/3
กับ
(sec2p/7)1/3+(sec4p/7)1/3+(sec6p/7)1/3={8-6*(7)1/3}1/3
โอ้ว ยิงปืนทีเดียวในนกสองตัวเลยแหะ ^0^
ปล. โจทย์คุณ ZOHAN เถื่อนมาก >-<
| จากคุณ |
:
jesus_god  
|
| เขียนเมื่อ |
:
10 ส.ค. 52 07:18:53
|
|
|
|
 |