 |
ความคิดเห็นที่ 23 |
 |
ความคิดเห็นนี้ ผู้เขียน (kuzibimun) ได้พิจารณาแล้วว่าไม่ถูกต้อง ควรอ่าน #25, #26, #27 แทนครับ
--- ข้อความเดิม ---
#22 --- ผมเขียน #20 ไม่รัดกุมเองครับ ขออนุญาตอธิบายให้รัดกุมนะครับ
1/4 = 1/3 - 1/9 + 1/27 - 1/81 + ...
= (1/3-1/9) + (1/27-1/81)+ ...
= 2/9 + 2/9^2 + 2/9^3 + ...
=> 1/4 เขียนเป็นเลขฐาน 3 ได้ว่า 0.02020202...
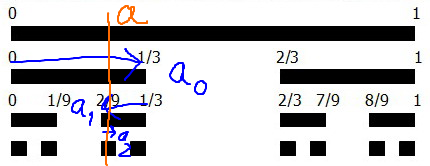
คราวนี้มาดูจุดปลายของ sequence of sets กัน (เขียนเลขฐาน3ทั้งหมด)
จุดปลายของ C_0 คือ 0, 1
จุดปลายของ C_1 คือ 0.0, 0.1, 0.2, 1
จุดปลายของ C_2 คือ 0.00, 0.01, 0.02, 0.1, 0.20, 0.21, 0.22, 1
...
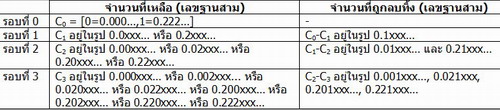
การหาจุดปลายของ set C_(n+1) เมื่อมีจุดปลายของ set C_n ทำได้โดย
ไล่จุดปลายของ C_n ทีละตัว
ถ้า least significant digit เป็น 1 ก็ลอกลงมาไว้เฉยๆ
(เช่น C_0 มี 1 ก็ลอก 1 มาไว้ที่ C_1 จบ
หรือ C_1 มี 0.1 ก็ลอก 0.1 มาไว้ที่ C_2 จบ)
ถ้า least significant digit ไม่เป็น 1 ก็เติมเลขเข้าไปทางขวาอีกหลักหนึ่ง แล้วก็เขียน 0 1 2 ตามลงไป
(เช่น C_0 มี 0 -> C_1 จะมี 0.0 0.1 0.2
หรือ C_1 มี 0.2 -> C_2 ก็จะมี 0.20 0.21 0.22
หรือ C_1 มี 0.0 -> C_2 ก็จะมี 0.00 0.01 0.02)
----
เพราะฉนั้น cantor set มีจุดปลายทุกจุดเขียนเป็นเลขฐาน 3 ได้เป็นรูป
0.a1 a2 a3 a4 ... (a_n ทุกตัว อยู่ในเซต {0, 1, 2})
โดยมีเงื่อนไขว่า ถ้า a_i ใดๆ เป็น 1, a_k จะต้องเป็น 0 สำหรับทุกๆ k > i
จุด 1/4 = 0.020202020202.... จึงเป็นจุดปลายของ cantor set
ถ้าผิดพลาดที่ใดก็ขอความกรุณาด้วยครับ
แก้ไขเมื่อ 09 ส.ค. 52 17:18:53
แก้ไขเมื่อ 09 ส.ค. 52 16:56:33
| จากคุณ |
:
kuzibimun 
|
| เขียนเมื่อ |
:
9 ส.ค. 52 16:34:42
|
|
|
|
|
... เข้ามาดู
