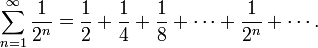ความคิดเห็นที่ 1 ก็ไม่รู้ว่าจะทำให้ใครหลายคนปวดหัวหนักขึ้นกว่าเดิมหรือเปล่า แต่ผมคิดว่าถ้าพวกเราช่วยกันคิดด้วยกันหลาย ๆ คน อะไร ๆ มันก็น่าจะชัดเจนขึ้น และน่าจะเป็นประโยชน์ครับ เนื่องจากช่วงนี้ ผมต้องใช้ภาษาอังกฤษโขอยู่ ความคิดในหัวช่วงนี้ ก็เลยเป็นเสียงในฟิลม์อยู่บ่อย ๆ แต่ก็มีประโยชน์อยู่เหมือนกัน เพราะมีหลายเรื่องที่คิดเป็นภาษาอังกฤษแล้ว จะชัดเจนกว่าคิดเป็นภาษาไทย (ดังนั้น ขออภัยล่วงหน้าด้วยครับ ถ้าภาษาผมช่วงนี้ มันจะแปร่ง ๆ ไปบ้าง) ด้วยความที่เป็นคนไทย ผมจึงมีโอกาสได้เห็นว่าเรามีข้อได้เปรียบฝรั่งอยู่บางประการ เวลาที่เราคิดถึงความหมายของคำในภาษาอังกฤษ (อ่านไม่ผิดหรอกครับ) อย่างนึงก็คือ เราจะไม่มองมันแบบเดียวกับภาษาของเรา คือเราจะมองมันคล้าย ๆ กับเวลาที่เรามองสมการคณิตศาสตร์ (ลองเขียนสมการยุ่ง ๆ ดู แล้วเปลี่ยนจากตัวแปร x, y, z เป็น ก, ข, ค ดู แล้วจะรู้สึกพิกล ๆ ยังไงก็ไม่รู้ ผมคิดว่าการที่ท่าน Euler ใช้ตัวอักษรกรีกแทนตัวแปร ก็น่าจะด้วยเหตุผลเดียวกันนี้เอง) แต่อีกทางนึง เราก็เสียเปรียบเขาอยู่เหมือนกัน เพราะว่าเราต้องแปล (และหลักข้อแรกที่ผมแนะนำผู้ที่อยากจะฝึกภาษาอังกฤษ ก็คือ อย่าแปล) การแปลนั้น ทำให้เสียความรู้สึก (sense) ที่เราจะมีต่อคำนั้น ๆ ไปได้เยอะอยู่เหมือนกัน จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 18:21:49

ความคิดเห็นที่ 2 เพื่อประโยชน์ในการสนทนา ก็จะขออนุญาตแปลคำต่าง ๆ ที่เกี่ยวข้องไว้พอสังเขปครับ ได้แก่ infinity = อนันต์ หรือจำนวนอนันต์ meaningless = ไร้ความหมาย, ไม่มีความหมาย undefined = ไม่(ได้ถูก)นิยาม(ไว้) indeterminant = หาค่าไม่ได้, ไม่สามารถหาค่าได้ ที่จริงแล้ว ผมไม่ค่อยชอบการแปลคำว่า undefined ว่า "ไม่นิยาม" สักเท่าไรนัก แต่ถ้าต้องแปล ก็คงใกล้เคียงที่สุดแล้ว เพราะมันจะสอดคล้องกับอีกคำ คือ definition หรือ "นิยาม" แต่ถ้าจะว่าไปแล้ว คำว่า undefined และ indeterminant นั้น ใกล้เคียงกันมาก จนเกือบจะแทนกันได้ เช่นเราจะพูดถึง indeterminant forms ที่รู้จักกันดีทั้งเจ็ดรูปว่าเป็น undefined forms หรือว่า undefined expressions ก็ได้เหมือนกัน ใน sense ของคำแล้ว indeterminant = not being able to determine (so we say it's undefined) undefined = something that was not defined (since it's meaningless) ---------------------------------------------- แก้ไข: ขอเพิ่มเติมในประเด็นที่คุณเซียนแห่งmath ทักมาใน #5 ซักหน่อยนะครับ เวลาที่เราใช้คำว่า undefined ในชีวิตประจำวันนั้น มันมีความหมายแค่ว่า สิ่งที่ไม่ได้ถูกนิยามไว้ (something that was not defined) แค่นั้น ทีนี้ (ยังเป็น context ทั่วไป นอกคณิตศาสตร์) ส่วนใหญ่แล้วนัยยะที่แฝงไว้ก็คือ ที่มันยังไม่ได้ถูกนิยามไว้ ก็เพราะว่าใครคนที่น่าจะเป็นคนให้นิยาม ไม่ยอมให้นิยาม ด้วยสาเหตุบางประการ (ที่คนที่พูดก็ไม่รู้เหมือนกัน) เช่น I don't know why it's undefined. He didn't define it, so it's undefined. I think he won't define it (= there's no way he will define it). Maybe he think it's not important enough. แต่ถ้าเราพูดถึงอนิยาม (undefined terms) ตาม #4 แล้ว มันจะหมายถึง สิ่งที่เราน่าจะรู้กันดี จึงไม่จำเป็นต้องนิยาม Undefined terms are undefined because we didn't and we won't define it. We don't see why it's necessary to (bother to) define them. (= everybody should already know what they are) แต่(อันนี้ความเห็นส่วนตัวนะครับ)ในความเห็นผม ผมคิดว่าคำว่า undefined ใน อนิยาม (undefined terms) นั้น มีความหมายต่างจาก undefined ใน something undefined อยู่เล็กน้อยครับ undefined terms ใช้ใน sense ของคณิตศาสตร์ แต่ something undefined นั้น ใช้ใน sense ของภาษาอังกฤษทั่วไปครับ. แก้ไขเมื่อ 10 ส.ค. 52 19:52:25 แก้ไขเมื่อ 10 ส.ค. 52 19:51:33 จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 18:22:55

ความคิดเห็นที่ 3 ทีนี้ ถ้าถามว่า 1/0 = ? แล้วพยายามตอบเลย (เช่น บางท่านอาจจะบอกว่ามันเป็น infinity บางท่านก็ว่ามัน undefined) มันก็จะยุ่ง เพราะมันขาดกรอบคิดไว้อ้างอิง (frame of reference) ครับ เพราะถ้าจะว่าไป ก็ถูกกันทั้งคู่ แล้วแต่กรอบที่กำลังคิด ว่าเป็นคณิตศาสตร์แขนงใด แต่ทีนี้ สมมติว่าเรามาลองคิดแบบม.ปลาย หรือป.ตรี กันดู ก็จะพบว่า 1/0 = infinity นั้น ไม่ถูก แต่เข้าใจได้ ทำนองเดียวกับที่เราได้ยินในหนังฝรั่งบ่อย ๆ ว่า You all right? ซึ่งถ้าไปถามครูภาษาอังกฤษ รับรองโดนดุ เพราะมันไม่ถูกหลักภาษา แต่เราก็เข้าใจได้ว่า คนที่พูด เขาหมายถึง Are you all right? ทำนองเดียวกับที่เราก็เข้าใจได้ว่า 1/0 นั้น ก็คือ limit ของ 1/x เมื่อ x มีค่าเข้าใกล้ 0 นั่นเอง ซึ่งยิ่ง x มีค่าเข้าใกล้ 0 มากเท่าไหร่ 1/x ก็ยิ่งมากขึ้นเท่านั้น จึงพอจะอ้างได้ว่า limit ของ 1/x เมื่อ x มีค่าเข้าใกล้ 0 จึงมีค่าเป็น infinity แต่ถ้าคิดดูอีกที ก็จะพบว่า แม้กระทั่ง limit 1/x เมื่อ x -> 0 นี้ ก็ไม่สามารถหาค่าได้ เพราะว่า limit ทางซ้าย และทางขวานั้น ไม่เท่ากัน limit ของ 1/x เมื่อ x -> 0 ก็เลย undefined หรือ indeterminate นั่นเอง จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 18:47:39

ความคิดเห็นที่ 4 1.  โครงสร้างของวิชาคณิตศาสตร์     ประกอบด้วยส่วนที่สำคัญ  4  ประการคือ       1.1  อนิยาม (Undefined  Term)  หมายถึง   คำที่ไม่ให้ความหมายหรือ คำจำกัดความแต่ให้ความเข้าใจตรงกัน  นักคณิตศาสตร์ได้เริ่มโครงสร้างวิชาคณิตศาสตร์ด้วยคำกลุ่มหนึ่ง  ซึ่งไม่ให้ความหมายหรือคำจำกัดความ  โดยที่ให้ตกลงกันว่าคำเหล่านี้เป็นที่เข้าใจ  อาจทำความเข้าใจให้ตรงกันโดยใช้วิธียกตัวอย่างหรือเข้าใจด้วยปฏิภาณ  ตัวอย่างของอนิยาม  ในวิชาคณิตศาสตร์  เช่น  จุด  ค่าคงที่  เท่ากัน  มากกว่า  เซต  ระนาบ  ฯลฯ  อนิยามเหล่านี้มีจำนวนน้อยที่สุดเท่าที่จะเป็นไปได้     1.2  นิยาม (Definition  หรือ  Defined  Term)  คือ  การเอานิยามมาบรรยาย  หรือกำหนดคุณลักษณะของสิ่งใดสิ่งหนึ่ง  เช่น  เราเอาคำว่า  “จุด”  และ  “ทางเดิน”  มาอธิบายคำว่า  “เส้น”  เช่น  “เส้นคือทางเดินของจุด”  เราใช้ว่า  “เส้น”  ไปนิยามคำว่าเส้นตรง  เส้นขนาน  เราใช้ “เซต” ไปใช้นิยามสับเซต  ดังตัวอย่างสิ่งที่ต้องนิยามในวิชาคณิตศาสตร์  เช่น  ตัวหารร่วมมาก  วงกลม  สับเซต  ฯลฯ    1.3  สัจพจน์หรือกติกา (Axioms  หรือ  Postulate) หมายถึง  ประโยคหรือข้อความที่เราไม่ต้องพิสูจน์  แต่ยอมรับว่าเป็นจริงในเรื่องที่เราพูดกันอยู่  ในชีวิตจริงเรายอมรับอะไร ๆ หลายอย่างในลักษณะเป็นข้อตกลงหรือกติกา  เช่น  ยอมรับว่าการฆ่าสัตว์เป็นบาป  การแข่งขันกีฬาแต่ละชนิดมีกติกา  เพื่อให้ทุกคนยอมรับโดยไม่โต้แย้ง  กติกามักจะแสดงความสัมพันธ์ของนิยาม  หรืออนิยามที่เป็นพื้นฐานมาก  จนไม่สามารถพิสูจน์ได้  เช่น  กำหนดจุดสองจุด  จะลากเส้นตรงผ่านได้เพียงเส้นเดียว  เส้นขนานย่อมไม่ตัดกัน     1.4  ทฤษฎีบท (Theorem)  เป็นผลสรุปที่ได้จากข้อมูลชุดหนึ่ง  หรือจากเงื่อนไขที่กำหนด  สามารถพิสูจน์ได้ว่าเป็นจริง  (Valid) ทุกกรณี  คือ  สมเหตุสมผล  การพิสูจน์ทฤษฎีเป็นการให้เหตุผลทางตรรกวิทยา  โดยการนำเอานิยาม  กติกา  หรือทฤษฎีบทที่ได้พิสูจน์แล้วไปสนับสนุนเป็นเหตุเป็นผลเพื่อแสดงว่าทฤษฎีนั้นเป็นจริง (Fact  หรือ  Truth)  แต่ที่ทฤษฎีทางคณิตศาสตร์บางแขนง  บางเรื่องที่เป็นข้อเท็จจริงทุกกรณี  ทั้งนี้ขึ้นอยู่กับกติกาของคณิตศาสตร์แขนงนั้น  ถ้ากติกาเป็นข้อเท็จจริงแน่นอน  ทฤษฎีที่พิสูจน์โดยกติกานั้นอ้างอิงเป็นเหตุเป็นผล  ก็ย่อมได้ผลเป็นข้อเท็จจริงด้วย จากคุณ : เซียนแห่งmath เขียนเมื่อ : 10 ส.ค. 52 18:58:02

ความคิดเห็นที่ 5 อนิยามไม่ได้หมายความว่ามันไม่มีความหมาย จากคุณ : เซียนแห่งmath เขียนเมื่อ : 10 ส.ค. 52 18:58:45

ความคิดเห็นที่ 6 นิยามเกี่ยวค่าของ limit ที่ใช้ ๆกันเท่าที่ผมรู้มี Limit exists Limit doesn't exists Limit converges to Limit diverges to +ฅ Limit diverges to -[infinity] สมัยเรียนวิชาอย่างพวกแคลคูลัสเราไม่ได้สนใจข้อตกลงอะไรกันมากนัก สนใจเพียงวิธีการ การให้ได้มาซึ่งคำตอบ แต่ถ้าเรียนวิชาอย่าง analysis ต้องเลือกใช้คำให้ถูกต้องตามนิยาม จากคุณ : เซียนแห่งmath เขียนเมื่อ : 10 ส.ค. 52 19:05:03

ความคิดเห็นที่ 7 ทีนี้ มันก็มีเหมือนกันที่บางเรื่อง คณิตศาสตร์คนละแขนงจะแย้งกันเองอย่างสิ้นเชิง อย่างเช่น 00 ซึ่งส่วนใหญ่จะให้มันเป็นสิ่งที่ undefined แต่ผมชอบที่ Knuth เคยแย้งไว้ (ในกรอบของ Computing Mathematics) ว่า 00 = 1 ต่างหาก (ท่านที่สนใจ ลองค้นเอาจากเว็บก็ได้ ไม่น่าจะหายากครับ) สรุปคือ โดยความเห็นส่วนตัวแล้ว ผมคิดว่าถ้าไม่มีกรอบคิดอ้างอิงที่ตรงกัน (จะเรียกว่า frame of reference ก็ได้ หรือ context ก็ได้) การพูดถึง infinity, undefined, indeterminate ในหลาย ๆ กรณีนั้น meaningless ครับ.    ปล. เวลาที่ผมคิดถึงคำว่า meaningless ในที่นี้ ผมคิดถึงมันในแง่ not meaningful    และในภาษามนุษย์แล้ว not ไม่ได้ตรงกันข้ามอย่างสิ้นเชิง    อย่างเช่น "I don't love you." นั้น ไม่ได้เหมือนกับ "I hate you." ครับ    ปลล. ท่านที่ภาษาอังกฤษแข็งแรงหน่อย จะนึกถึง meaningless ในที่นี้    ว่า = not entirely meaningful (so it has some meanings)    แต่ไม่ได้หมายถึง unmeaningful completely (so it has no meaning at all) ครับ. จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 19:05:07

ความคิดเห็นที่ 8 lim f(x) = f(a) หมายความว่า f(x) เข้าใกล้ f(a) ขณะที่ x เข้าใกล้ a การเขียนสัญลักษณ์ทางคณิตศาสตร์ว่า  1/x เข้าใกล้ 1/0 เมื่อ x เข้าใกล้ 0 กับ 1/0 นั้นมีความหมายที่แตกต่างกัน ในหนังสือ Handbook of writting for mathematical science บทที่5 When English is a foreign language กล่าวถึงคำและการใช้ ภาษาอังกฤษ ในความหมายของคณิตศาตร์ แต่ผมยังอ่านไม่จบเลยเล่มนี้ อิอิ แก้ไขเมื่อ 10 ส.ค. 52 19:12:38 จากคุณ : เซียนแห่งmath เขียนเมื่อ : 10 ส.ค. 52 19:10:45

ความคิดเห็นที่ 9 #6 ขอบคุณครับคุณเซียนแห่งmath ที่ท้วงมา จริงอยู่ครับว่า pattern ของความภาษาอังกฤษในตำราคณิตศาสตร์ส่วนใหญ่แล้ว จะใช้คำว่า limit exists หรือ limit does not exists (ที่จริงยังมีอีก pattern คือคำว่า limit is fail to exist) แต่ว่าทำไมมันจึงไม่ exist? ไม่ใช่เพราะว่ามันเป็นสิ่งที่เราหาค่าไม่ได้ (indeterminate) หรอกหรือครับ จริงมั้ย :-) ทีนี้เผื่อไว้ว่าอาจจะกังวลว่าผมคิดภาษาอังกฤษ ไม่เหมือนคนอังกฤษจริง ๆ ก็ลองดูที่นี่ได้ครับ http://mathworld.wolfram.com/Indeterminate.html ในนั้น มีประโยคนึงเขียนว่า For example, a limit of the form 0/0, i.e., lim_(x->0)f(x)/g(x) where lim_(x->0)f(x)=lim_(x->0)g(x)=0, is indeterminate ... จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 19:19:48

ความคิดเห็นที่ 10 จดๆๆๆๆๆ จากคุณ : หมึกสด เขียนเมื่อ : 10 ส.ค. 52 19:29:48

ความคิดเห็นที่ 11 #8 ถ้าจะให้ถูกต้องตามหลักแล้ว limit ของ 1/x เมื่อ x เข้าใกล้ 0 นั้น เป็นคนละสิ่งกับ 1/0 จริง ๆ (เวลาที่เห็นใครเขียน 1/0 นั้น ชวนให้นึกถึง (ตอนนี้คิดเป็นไทยแล้ว) เวลาทักกันว่า "บายดีป่ะ" ซึ่งถ้าเขียนอย่างนี้ในวิชาภาษาไทย ก็คงโดนเขกหัวเป็นแน่) แต่ผมมีข้อสังเกตส่วนตัวประการนึงครับ คือ 1/0 นั้น ไม่ยักกะอยู่ใน seven indeterminate forms แฮะ (ส่อนัยยะว่า ในหลาย ๆ context แล้ว มันไม่ใช่สิ่งที่ indeterminate). แก้ไข: แปะเบอร์คคห.ผิดครับ แหะ ๆ แก้ไขเมื่อ 10 ส.ค. 52 19:36:43 จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 19:36:06

ความคิดเห็นที่ 12 ถูกตามที่ลุงแว่นว่าแหละครับ ถ้าเราสามารถ determine ค่าออกมาได้ ก็ถือว่า exists ขอเพิ่มเติมในข้อพิจารณาต่อไปนี้ซึ่งมันมีความแตกต่างกันในแง่ของความหมาย a limit of the form 0/0 a limit of 0/0 บ่อยครั้งที่ผมอ่านกระทู้ ตอบกระทู้ เราถกเถียงกัน ปัญหาจริง มันเกิดจากความไม่รัดกุม ทั้งของผู้เขียนและผู้อ่าน ทำให้มันมีคำถามมาว่าแล้วถ้าแบบนั้น แบบนี้ ถ้าเขียนไม่รัดกุม มันจะขึ้นกับการตีความของผู้อ่าน ว่าจะเข้าใจเหมือนกับที่ผู้เขียนวาดภาพไว้ในใจหรือไม่ จากปัญหาคณิตศาสตร์ มันจบแบบปัญหาทายใจ แก้ไขเมื่อ 10 ส.ค. 52 19:42:25 แก้ไขเมื่อ 10 ส.ค. 52 19:40:35 จากคุณ : เซียนแห่งmath เขียนเมื่อ : 10 ส.ค. 52 19:37:57

ความคิดเห็นที่ 13 กลับมาแล้ววววววววววววววววววววว ^^ จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : 10 ส.ค. 52 19:39:19

ความคิดเห็นที่ 14 ^ เอาเป็นว่าแวะเข้ามาชวนคุย เฉพาะวันนี้ก่อน ก็แล้วกันครับ คิดถึงทุก ๆ คนนะครับ :) จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 19:58:39

ความคิดเห็นที่ 15 คิดว่าจะตั้งกระทู้แบบนี้แหละ ต่อจากกระทู้โจทย์ที่ถามเมื่อวานค่ะ http://www.pantip.com/cafe/wahkor/topic/X8179827/X8179827.html แต่คงทำได้ไม่ดีเท่าคุณลุงแว่นใจดีตั้งแน่ๆ ขอทำหน้าที่ผู้ซักถามแล้วกันค่ะ ^^ การหารด้วย 0 มิ้นเข้าใจว่าตอบว่า "ไม่นิยาม"  คำว่าไม่นิยามในความหมายหมายถึง การเอามันออกจากระบบ ไม่นำมาคิด เพราะจะทำให้เกิดเรื่องยุ่งๆ เช่น 1x0=2x0 หาร 0 ทั้งสมการ 1 = 2 ยุ่งแล้วค่ะ เช่น 2infinity= infinity+a ลบ infinityสองข้าง infinity  = a ยุ่งแล้วค่ะ แต่เราจึงนิยมใช้พวกไม่นิยามทั้งหลายในเรื่องของ limit เพื่อให้ ทำความเข้าใจมันได้มากขึ้น ส่วน infinity นั้น ไม่ได้เป็นจำนวน แต่เป็นสัญลักษณ์ และถูกกำกับด้วยนิยาม จึงไม่สามารถนำมาบวกลบคูณหารกันได้ในระบบจำนวนจริง คิดแบบนี้ถูกไหมคะ จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : 10 ส.ค. 52 20:05:33

ความคิดเห็นที่ 16 ^ ถ้าเอาแบบสั้น ๆ ผมคิดว่าที่คุณ mint_la ว่ามาโดยรวมนั้น ก็ถูกแล้วครับ คือ แต่ทว่าต้องตั้งอยู่ในกรอบคิด (context) ที่คุณมิ้น ๆ คิดอยู่ (ถ้าผมเข้าใจไม่ผิด คิดว่ามีบางสำนัก ที่เขาถือว่า 1/0 = infinity แต่โดยส่วนใหญ่แล้ว จะถือว่ามัน undefined) ส่วน infinity นั้น มันเป็นอะไรบางอย่าง ที่มากจนไม่รู้จะมากยังไง บางคนอาจให้นิยามมันว่า infinity เป็นจำนวนจริงที่มากที่สุด (แล้วจำนวนที่มากที่สุด ของเซตที่สมาชิกไม่จำกัด (infinite set) มันจะมีมั้ยเนี่ย?) ส่วนบางคน อาจนิยามมันว่ามันเป็น unbounded limit (ผมเจอใน wiki) คำว่า limit แฝงนัยยะว่ามันหาค่าได้ (determinate) มัน bound มัน converged แล้วไอ้เจ้า unbounded limit นี่มันหน้าตายังไงล่ะ? งงดีมั้ย หึหึ จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 20:24:04

ความคิดเห็นที่ 17   1/0 = เหตุก่อนมีตัวเลข ดังนั้นจะนิยามลงไปมันก็ผิด เพราะมันมาก่อนสัญลักษณ์ แต่ไม่ใช่ว่าไม่มี จากคุณ : หลับตา เขียนเมื่อ : 10 ส.ค. 52 20:36:49 A:58.64.63.12 X: TicketID:173601

ความคิดเห็นที่ 18 ทีนี้ ขออนุญาตเจาะลึกนิดนึง ในประเด็นที่ว่า ทำไมผมจึงรู้สึกว่า undefined กับ indeterminate จึงต่างกันมาก ทั้ง ๆ ที่ในปัจจุบันนี้ สองคำนี้แทบจะใช้แทนกันได้อยู่แล้ว เวลาใช้เป็น adj. ผมคิดว่ามันอยู่ที่มุมมองของบุคคลนั้น ๆ เวลาคิดถึงสิ่งที่เรา "ไม่มีนิยาม/หาค่าไม่ได้" ครับ (ถึงแม้ว่าต่างก็กำลังพิจารณาสิ่งเดียวกัน ก็ตามที) ยกตัวอย่างเช่น คำว่า hair ถ้าเรามองผมทั้งหัว เราก็จะบอกว่ามันเป็นคำนามนับไม่ได้ (เพราะว่านับกันไม่หวาดไม่ไหว) แต่ถ้าเรามองเส้นผมบนหัวแต่มองไปที่แค่ไม่กี่เส้น (เช่นเวลาถอนหงอก) เราก็จะใช้คำว่า hairs เพราะว่าเรานับได้แล้ว ใน sense แล้ว ผมมองว่า สำหรับนักคณิตศาสตร์ที่มุ่งค้นหาว่าโลกเป็นอย่างไร จะใช้คำว่า indeterminate โดยอัตโนมัติ เพราะว่าพอเจอ 0/0 เข้าให้ ก็ไม่รู้ว่าจะหาค่าออกมาได้อย่างไร (คือ หมดความสามารถที่จะหา) แล้วค่อยไปคิดถึงว่า มันมี หรือไม่มีนิยามหรือไม่ กันทีหลัง ส่วนนักคณิตศาสตร์ที่เน้นกฎระเบียบเป็นที่ตั้ง จะเลือกใช้คำว่า undefined โดยอัตโนมัติ เพราะว่าในความเห็นท่าน ไม่มีอะไรที่มีอยู่ จนกว่าเราจะต้องให้นิยาม (define) มันเสียก่อน และแน่นอนว่าไม่เคยมีใคร define 0/0 มาก่อน มันจึงเป็นสิ่งที่ undefined ดังนั้น เราอาจพูดได้ว่า 0/0 นั้น มัน undefined  ก็เพราะว่าที่จริงแล้ว มัน indeterminate ซึ่งก็เป็นเพราะว่ามัน undefined    เพราะว่าที่จริงแล้ว มัน indeterminate ซึ่งก็เป็นเพราะว่ามัน undefined      เพราะว่าที่จริงแล้ว มัน indeterminate ซึ่งก็เป็นเพราะว่า มัน undefined        ... ปล. ตอนนี้ผมชักรู้สึกว่า เจ้า paragraph ข้างบนนั่นมัน meaningless หน่อย ๆ แล้วล่ะ :) จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 10 ส.ค. 52 20:39:43

ความคิดเห็นที่ 19 inw จากคุณ : siLvan เขียนเมื่อ : 10 ส.ค. 52 20:50:17

ความคิดเห็นที่ 20 โดยส่วนตัวเวลาผมเห็น 1/0 ผมจะถูกทำให้ยึดติดกับความคิดสองอย่างในหัว 1. error devided by zero 2. มันน่าจะมีค่ามาก ถ้ามันจะมีอยู่ หรือ ถ้าเราจะยอมให้มันมีอยู่ แต่พอทบทวนขึ้นจริง การที่ ทำให้ 1/0 มีค่าขึ้นมา เท่ากับเปนการพังทลาย ระบบคิดเดิมทั้งหมด ทุกๆ เอกลักษณ์ จะหมดสิ้นไป หากเรายอมรับความมีอยู่ของ 1/0 หรือ อีกหลายๆตัว จากคุณ : อ๊อดบ้านโป่ง (Santa_Baby) เขียนเมื่อ : 10 ส.ค. 52 21:32:41

ความคิดเห็นที่ 21 ที่บางสำนักบอกว่า  1/0 = infinity อันนี้เป็นเรื่องที่เพิ่งทราบจริงๆเลย นึกว่าเข้าใจตรงกันหมดแล้วค่ะ กลับมาเรื่องใหม่ เรื่องของ หาค่าไม่ได้ กับไม่นิยาม มิ้นคิดแบบนี้ค่ะคุณลุงแว่น ไม่นิยาม เป็นส่วนหนึ่งของหาค่าไม่ได้ หาค่าไม่ได้ใหญ่กว่า หาค่าไม่ได้คือตอนเด็กๆ ที่พอเจอคำตอบอะไรแปลกๆก็จะบอกแล้วว่าหาค่าไม่ได้ เช่น sqrt(-1) หาค่าไม่ได้ infinity หาค่าไม่ได้ 1/0 หาค่าไม่ได้ แต่พอโตมาก็เริ่มรู้ว่าเค้ามีการแยกแยะ ประเภทของพวกหาค่าไม่ได้ออกเป็น หลายๆพวก เช่น sqrt(-1) = จำนวนจินตภาพ infinity หรือไม่นิยาม คำว่าไม่นิยาม อาจจะหมายถึง ยังไม่ได้นิยาม หรือไม่สามารถนิยามได้ มิ้นคิดว่าเป็นแบบหลังมากกว่า เพราะจะทำให้เกิดความยุ่งมากไปหมด เลยไม่ได้นิยามไว้น่ะค่ะ ทีนี้ก็ 0/0 ตอบว่า ไม่สามารถหาค่าได้ แบบไม่นิยาม(เพราะนิยามแล้วมันไปขัดแย้งกับแบบอื่น ) จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : 10 ส.ค. 52 21:43:19

ความคิดเห็นที่ 22 ขอโหวตให้ก่อน แก้ไขเมื่อ 10 ส.ค. 52 21:44:42 จากคุณ : nonlocality เขียนเมื่อ : 10 ส.ค. 52 21:43:57

ความคิดเห็นที่ 23 นิยามถึงสิ่งที่ว่างเปล่าอย่างแท้จริง และสิ่งที่หาที่สิ้นสุดไม่ได้อย่างแท้จริง ดูจะเป็นอะไรที่เหนือสามัญสำนึกของมนุษย์ในตอนนี้ จากคุณ : ทะเลคราม (blueocynia) เขียนเมื่อ : 10 ส.ค. 52 21:49:37

ความคิดเห็นที่ 24 ตอนที่คุณลุงแว่นใจดีไม่ได้เข้ามา มิ้นก็เคยตั้งกระทู้ประมาณว่า จะนิยาม 1/0 = 1mint 2/0 = 2mint อะไรแบบนี้น่ะค่ะ แล้วก็มีคนมาช่วยตั้งนิยามให้ จนสุดท้าย เกิดความขัดแย้งกับระบบเดิมมากจนเกินไป หากระทู้ไม่เจอแล้ว ^^ จำไม่ค่อยได้ ประมาณนี้มั้งคะ mint^2 = (1/0)^2 = 1/0 = mint mint^a = mint (เพิ่มนิยาม) mint/mint = (1/0) x (0/1) = 1(เพิ่มนิยาม 0/0 = 1) 0 mint = 0(1/0) = 1 อ่าวขัดแย้งกับ 0 x อะไรได้ 0 อีก 555 (นิยามใหม่) จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : 10 ส.ค. 52 21:52:20

ความคิดเห็นที่ 25 ไม่ ค่อยมี ภาษามนุษย์เลยอ่ะ มึน ๆๆๆ จากคุณ : ไม้โมก เขียนเมื่อ : 10 ส.ค. 52 22:33:27

ความคิดเห็นที่ 26 ผมนึกถึงเรื่องของคำสั่งที่ไร้ผล แล้วให้ค่าเท่ากับไม่มีค่าใดๆ ซึ่งตัวนี้ไม่ใช่ 0 เพราะ 0 คือมีค่าเท่ากับ 0 ถ้าเปรียบเทียบกับสัญลักษณ์ทางคณิตศาสตร์คงจะใกล้เคียงกับ เซตว่าง ประมาณว่ามีผลไม้อยู่ 50 ผลแบ่งออกไปลังละ 0 ผลอยากทราบว่าจะแบ่งได้กี่ลัง เมื่อพิจารณาแล้ว การจะแบ่งลังละ 0 ผลนั้นไม่ได้ทำให้ 50 ผลนั้นลดลงไปเลย ทำให้คำสั่งนี้ไร้ผลโดยปริยาย แล้ว 50 ผลนั้นก็ยังคงมี 50 ผลเช่นเดิม แต่ไม่สามารถผ่านกระบวนการนี้ไปได้ กลายเป็นกระบวนการที่เหตุไม่สามารถนำไปสู่ผล จึงการเป็นคำสั่งที่ไร้ผลไป จากคุณ : ทะเลคราม (blueocynia) เขียนเมื่อ : 10 ส.ค. 52 22:38:02

ความคิดเห็นที่ 27 มองว่า ศูนย์หรืออนันต์ เป็นที่สุดในธรรมชาติอันคือความจริงสิ้นเชิงที่ครอบคลุมลักษณะใดในธรรมชาติเสมอ ทั้งยังเป็นอิสระไม่อยู่ภายใต้กฎเกณฑ์ทางคณิตศาสตร์โดยทั่วไป(แต่เรามักสมมุติค่าศูนย์หรืออนันต์มาอยู่ในกฎเกณฑ์ทางคณิตศาสตร์ที่เราใช้ในชีวิตประจำวัน จึงเกิดปัญหาที่หาที่ลงเอยกันไม่ได้อยู่ทุกวันนี้ :) ตัวอย่างการกำหนดให้ศูนย์หรืออนันต์อยู่ภายใต้กฎเกณฑ์ของบวกลบคูณหาร  เช่น 0 * 5   =  0 * 7    ดังนั้นตามกฎของการคูณ   5 = 7    ??? ฅ + 6   =  ฅ + 2  ดังนั้นตามกฎของการบวก  6 = 2   ??? 0/8  =  0/5  ดังนั้นตามกฎของการหาร  8 = 5   ??? ฯลฯ จากคุณ : ผู้ศึกษา เขียนเมื่อ : 10 ส.ค. 52 23:21:37

ความคิดเห็นที่ 28 คณิตศาสตร์ช่างลึกซึ้ง ^ ^" จากคุณ : Mr.Learning เขียนเมื่อ : 10 ส.ค. 52 23:26:25

ความคิดเห็นที่ 29 ... undefined ( เช่น 0/0 ) สำหรับผมจะแปลว่า ยังไม่ได้นิยามและวิธีในการหาซึ่งผลลัพธ์ หรือวิธีที่มีอยู่ในปัจจุบันยังไม่สามารถหาค่าของมันได้เลย indeterminate ( ใน indeterminate form ทั้งหลาย ) สำหรับผมจะแปลว่า ยังไม่ได้กำหนดค่า ( ไม่ใช่หาค่าไม่ได้นะครับ ) อาจจะมีค่าของมันอยู่ใน context หนึ่ง ๆ แต่อาจจะไม่เท่ากันใน context อื่น ๆ แก้ไขเมื่อ 10 ส.ค. 52 23:50:32 จากคุณ : Mr. Fusion เขียนเมื่อ : 10 ส.ค. 52 23:48:11

ความคิดเห็นที่ 30 ขอตอบตามความคิดส่วนตัว (ไม่มีอะไรอ้างอิง) อนันต์ (infinity) เป็นสิ่งที่ไม่มีจริงในปัญหาทางกายภาพ เราสมมุติมันขึ้นมา เพื่อบอกว่า มัน เป็นสิ่งที่ใหญ่มาก ๆ เทียบกับสเกลของสิ่งที่สนใจอยู่ ในทางคณิตศาสตร์ด้านการคำนวณเชิงเลข การคำนวณที่เกี่ยวกับ เลขอนันต์ ก็เป็นการแทนค่าตัวเลขที่มากที่สุดที่สามารถคำนวณได้ ในสมการเชิงเลขที่พิจารณา ไม่นิยาม (undefined), หาค่าไม่ได้ (indeterminate) และสิ่งที่ไร้ความหมาย (meaningless) เป็นคำเฉพาะใน หนังสือ คณิตศาสตร์ ไม่มีความพิเศษในทางกายภาพ จากคุณ : nonlocality เขียนเมื่อ : 11 ส.ค. 52 00:19:20

ความคิดเห็นที่ 31 ขออภัย คุณ Mr. Fusion ตอนแรกคิดว่า ยังไม่มีใครเห็น จึงลบข้อความ ความคิดเห็นผิด ๆ ของผมที่เขียนไว้ เมื่อคุณ Mr. Fusion กลับมาตอบใน คห ที่ 33 จึงขอนำความเห็นที่ผิดของผมกลับมาโพสต์ (เพื่อมิให้ผู้อื่นสับสน) ------------ ข้อความเดิม ---------------- เพิ่มเติม ขอแย้ง คุณ Mr. Fusion #29 0/0 เป็นรูปแบบไม่กำหนด ( Indeterminate form ) รูปแบบหนึ่งใน 7 แบบ อ้างอิงจาก http://en.wikipedia.org/wiki/Indeterminate_form แก้ไขเมื่อ 11 ส.ค. 52 01:22:11 แก้ไขเมื่อ 11 ส.ค. 52 00:29:10 จากคุณ : nonlocality เขียนเมื่อ : 11 ส.ค. 52 00:23:20

ความคิดเห็นที่ 32 #29 แปลได้เยี่ยมทีเดียวครับ ที่จริง ผมก็ไม่อยากแปลคำว่า indeterminate ว่า = หาค่าไม่ได้ เท่าไหร่เหมือนกันครับ แต่คิดว่ามันใช้ได้ดีในระดับนึงเลยทีเดียว เพราะคำมันยังดิ้นได้พอ ๆ กับคำอังกฤษ คือ indeterminate = การที่เราหาค่ามันไม่ได้ (cannot determine its value) ทั้งนี้ ไม่ใช่ใน sense ว่ามันไม่มีค่าอะไรเลยนะครับ แต่ว่าเป็นใน sense ที่ว่า เราหา (determine) ค่า หรือกำหนดค่ามันไม่ได้ต่างหาก ดังนั้น การที่มันอาจจะมีได้หลาย ๆ ค่า เช่น ถ้าเราคิดถึง a/0 ว่า = a/x เมื่อ x -> 0 จากมุมมองของ limit เราก็จะพบว่า limit มัน indeterminate เพราะ limit ทางซ้ายไม่เท่ากับ limit ทางขวา คือมันเป็นได้ทั้ง +infinity และ -infinity เราจึงชี้ขาดลงไปไม่ได้น่ะครับ ขอให้ข้อสังเกตนิดนึงด้วยครับว่า ปัจจุบันเราใช้รูปประโยคว่า limit [ของ ...] does not exist ได้อย่างเป็นธรรมชาติมาก ๆ เวลาที่ limit ซ้าย กับ limit ขวาไม่เท่ากัน ทั้ง ๆ ที่มันไม่ได้ does not exist เพราะว่ามันเป็น nothing แต่เพราะว่ามัน can be many things ต่างหาก ทั้งนี้ เพราะมีการให้นิยามไว้แล้วว่าถ้า limit ซ้าย-ขวา ไม่เท่ากัน limit ก็ไม่ exist นั่นเองครับ. แก้ไข: พิมพ์คำว่า indeterminate มาก ๆ เข้า พอเวลาจะพิมพ์คำว่า determine บ้าง ดันกลายเป็น determinate ไปซะอย่างงั้นเลย :) แก้ไขเมื่อ 11 ส.ค. 52 00:56:34 จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 11 ส.ค. 52 00:32:16

ความคิดเห็นที่ 33 ... #31 0/0 เป็นเป็นตัวอย่างของ undefine ที่ง่ายที่สุดครับ ต้องดูด้วยว่ามันอยู่ใน context อะไร ถ้า 0/0 อยู่ในเรื่องของ limit มันจะกลายเป็น indeterminate form อย่างที่คุณว่าไว้ครับครับ แต่ถ้า 0/0 อยู่ในการบวกลบคูณหารธรรมดา ไม่มี limit เข้ามาเกี่ยว ก็ไม่อยู่ใน indeterminate form ครับ แต่จะเป็น undefine แทน เหตุผลที่ 0/0 ไม่นิยาม เพราะยังไม่มีวิธีหาผลลัพธ์ใด ๆ ที่น่าพอใจครับ วิธีหาผลลัพธ์ที่มีอยู่ในปัจจุบันหาค่าได้นะครับ แต่.... ผลออกมายอมรับไม่ได้ เขาเลยไม่ยอมรับ ตัว indeterminate form เองถ้ามองให้ดีคุณก็จะเห็นว่ามันเกิดจากปัญหารูปแบบ เดียวกันหมดเลยครับ คือ ปัญหา "การหารด้วยศูนย์" ทุกรูป ถ้าแตกออกมาจะมีองค์ประกอบที่เป็น เศษส่วนที่มีตัวหารเป็น 0 ทั้งนั้นเลยครับ ปัญหาแบบนี้มีระดับความยากแบบเดียวกัน ถ้าคุณแก้ปัญหาตัวนึงได้ ที่เหลือก็แก้ได้ด้วยครับ จากคุณ : Mr. Fusion เขียนเมื่อ : 11 ส.ค. 52 00:39:06

ความคิดเห็นที่ 34 undefined term นั้นเป็นโครงสร้างคณิตศาสตร์ การหารด้วยศูนย์เป็น undefined  เพราะการเขียน ในรูปของเศษส่วนมันสมมูลกับการหาร อะไรก็ตาม ที่อยู่ในรูป ratioมันจะนิยามทุกจุด ยกเว้นจุดที่ เป็น 0 เพราะเรานิยามการหารเป็นการคูณด้วยอินเวอร์ ซึ่ง 0 เป็นสมาชิกที่ไม่มีอินเวอร์ส การหารด้วยศูนย์ จึงเป็นข้อตกลงที่ยอมรับว่ามันเป็นอนิยาม อนิยามไม่ได้หมายถึงเราไม่สามารถหาค่ามันของมันได้ แต่มันหมายถึงเราไม่สามารถให้คำนิยามที่มันรัดกุม well-defined เช่นเดียวกับ จุด และ เส้น หรือ เซต เราไม่สามารถให้คำนิยามที่มันรัดกุมได้ มันจึงเป็นอนิยาม แม้รากศัพธ์ทางภาษามันจะให้ความหมายคล้ายคลึงกับ indeterminate แต่ในแง่ของโครงสร้างมันไม่ได้มาจากที่มัน indeterminate หรือ can't evaluate แต่มันมาจาก it's not well-defined เราถึงใช้undefined แก้ไขเมื่อ 11 ส.ค. 52 14:49:07 จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 00:51:55

ความคิดเห็นที่ 35 #30 สวัสดีครับ คุณ nonlocality คิดว่าไม่มีอะไรแย้งครับ โดยเฉพาะอย่างยิ่งในประเด็นทางคณิตศาสตร์ แต่ขอแย้งนิดนึงครับว่า ทั้ง 4 คำในหัวกระทู้นั้น เป็นคำที่ใช้ได้ในชีวิตประจำวันทั้งหมดครับ แม้กระทั่งคำว่า indeterminate ซึ่งอาจจะไม่ค่อยคุ้นหูกันอยู่สักหน่อยก็ตาม ถ้าใช้แบบทั่วไป indeterminate ก็ยังคงหมายความว่า not determined ครับ ไม่ว่าจะเป็นเพราะ was not determined, cannot determine, will not determine ก็ตาม เพียงแต่ว่าความหมายของ determine ก็จะเลื่อนจาก การกำหนดค่า (เชิงคณิตศาสตร์) ไปเป็น การกำหนดอะไรสักอย่างเอาไว้ครับ (เช่น หมายกำหนดการ หรือชะตาชีวิตของใครสักคน เป็นต้น) ดังนั้น ถ้าแปล คำแปลก็จะค่อนไปทางว่า indeterminate = กำหนดไม่ได้, ไม่ได้กำหนดไว้, ยังไม่กำหนด อะไรทำนองนี้ครับ ส่วนคำว่า define, defined, undefined นั้น อาจพบได้บ่อย ๆ ในหนัง เช่น Man 1: Are you sure you want to get involved? Man 2: Define "get involved". นี่แปลว่านาย Man 2 ไม่แน่ใจว่า Man 1 หมายถึงอะไรเวลาที่พูดว่า "get involved" ครับ (หมายเหตุ: ถ้าเป็นหนัง แล้วคนเขียนบทเจ้าเล่ห์เล็กน้อย อาจให้ Man 1 ย้อน Man 2 คืนบ้างก็ได้ เช่น Man 1 : Define it yourself smart a$$. To me, it is something undefined.) วันนี้ ผมคงต้องขอตัวแต่เพียงเท่านี้ครับ ขอเชิญท่านอื่น ๆ ให้ความเห็นเพิ่มเติมได้ตามสะดวกนะครับ ถ้าพรุ่งนี้มีเวลา ผมจะแวะเข้ามาดูบ้างครับ ขอบคุณทุกท่านครับ :) แก้ไข: ขอแก้คำว่า get involve เป็น get involved ครับ ลองอ่านที่ตัวเองเขียน เลยสังเกตเห็นว่าถ้าสมองไม่แล่นนัก จะเขียนว่า get involve แปลว่า ในเวลาปกตินั้น สมองผมต้องคิดเป็นคำว่า get involve แล้วจะมีสมองอีกส่วน (ซึ่งจะไม่ค่อยทำงาน เวลาง่วง) มาคอยเตือนว่าต้องเป็น get involved ต่างหาก น่าสนใจดีเหมือนกันแฮะ แก้ไขเมื่อ 11 ส.ค. 52 01:06:38 จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 11 ส.ค. 52 00:52:46

ความคิดเห็นที่ 36 INFINITY   is  defined  as  a very very big quantity  which  is indeterminant. แก้ไขเมื่อ 11 ส.ค. 52 01:02:28 จากคุณ : sb*star เขียนเมื่อ : 11 ส.ค. 52 00:57:42

ความคิดเห็นที่ 37 เมื่อมาถึงระบบพิศดารอย่างลิมิต มันจำต้องขยายระบบจำนวนจริงออกไป เพื่อรองรับเจ้าตัว infinity จึงมีบางส่วนที่นิยาม เพิ่มตามที่คุณ mint เคยโพสไว้ นักคณิตศาสตร์เขาขยายระบบออกไป แต่ยังคงระบบเดิมไว้ มันจึงไม่ใช่ระบบใหม่ในคณิตศาสตร์ ลิมิตยังคงสอดคล้องกับ Real number system อยู่ 0/0 ก็ยังคงเป็น undefined 0/0 ไม่ใช่ indeterminated value แต่มัน isn't defined สมมติจำหนด f(x)/g(x)  เรากำกับไว้เสมอว่า g(x) ต้องไม่เป็น 0 ถ้าเป็น 0 เมื่อไหร่ จบการพิจารณา มันไม่อยู่ในระบบการพิจารณา แม้ระบบที่มีอินฟินิตี้อยู่แล้วเพราะระบบ extension Real system เป็นระบบขยายที่ระบบ Real system ยังคงจริงอยู่ แก้ไขเมื่อ 11 ส.ค. 52 01:15:16 จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 01:02:56

ความคิดเห็นที่ 38 เมื่อไหร่ที่คณิตศาสตร์สั่งให้คุณ determine คุณต้อง find with proof แต่เมื่อไหร่คณิตศาสตร์สั่งให้คุณ define คุณต้องเช็ค well-defined จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 01:05:27

ความคิดเห็นที่ 39 งานนี้ขอตีตั๋วคนดูครับ แต่ขออนุญาตค้านคุณ nonlocality นิดนึง (นิดเดียวจริง ๆ - นิดขนาดเท่ากับ 1/ฅ ใครจะตัดทิ้งก็ตัดทิ้งได้) ใน #30 (หรือความเห็นอื่นที่ใกล้เคียงกัน) ในแง่ที่ว่า อนันต์ (infinity) เป็นสิ่งที่ไม่มีจริงในปัญหาทางกายภาพ เพราะในทางกายภาพเราสามารถสร้างสามเหลี่ยมมุมฉากที่มีด้านประกอบมุมฉากยาวด้านละ 1 หน่วยได้ และเราจะเจอปัญหาด้านตรงข้ามมุมฉากในรูป x2 = 2 ทันที และเรารู้อีกด้วยว่า x = 21/2 ซึ่งเราพูดว่ามันเป็นจำนวนอตรรกยะ นี่ไงครับ มีอนันต์เข้ามาจริง ๆ ในปัญหาทางกายภาพแล้ว เพราะ 21/2 มีทศนิยมอนันต์ ผมคิดว่ากรณีนี้อนันต์ฟ้องความมีตัวตนของมันออกมาแล้วนะครับ จากคุณ : ศล เขียนเมื่อ : 11 ส.ค. 52 01:09:03

ความคิดเห็นที่ 40 ^ ไม่ได้เจอกันนานเลยนะครับ คุณศล อืมม์ ยกตัวอย่างได้เยี่ยมเลยครับ ทีแรกที่ผมอ่าน #30 ของคุณ nonlocality ผมเข้าใจไปว่า ที่คุณ nonlocality บอกว่าทั้ง 4 คำ "ไม่มีความพิเศษในทางกายภาพ" นั้น หมายถึงว่า คุณ nonlocality นึกไม่ออก หรือไม่เ็ห็นว่า 4 คำนี้ มีที่ใช้ในชีวิตประจำวันอย่างไร (ซึ่งผมคิดว่า มันมีที่ให้ใช้ได้ทั้ง 4 คำครับ) 21/2 เป็นการมองจากอีกมุมนึงจริง ๆ ปล. สบายดีนะครับ :) จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 11 ส.ค. 52 01:16:38

ความคิดเห็นที่ 41 เพิ่มอีกนิด infinity ในระบบ Extension ของจำนวนจริง ถือเป็น bound ของ จำนวนจริง R=(-ฅ,ฅ) จะกี่ infinity ก็ไม่ใหญ่ไม่กว่านั้นด้วยนิยาม แต่ไม่ได้หมายความว่ามันจริงทุกระบบตัวอย่างนึงคือ Cardinal ของ Z น้อยกว่า Cardinal ของ R จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 01:21:58

ความคิดเห็นที่ 42 #37 ขอถามคุณเซียนแห่งmath ในประเด็นที่คุณ mint_la สงสัยว่า infinity เป็นจำนวนหรือไม่ ผมคิดว่ามันเป็นได้ทั้ง เป็น และไม่เป็น แล้วแต่ context แต่จะค้นตำราหรือเอกสารอ้างอิง ก็ลำบากเหมือนกัน ไม่ทราบว่าในเรื่องระบบจำนวน (Number System) นั้น เขามีมุมมองหรือนิยามต่อ infinity ในประเด็นนี้ ว่าอย่างไรบ้างครับ (จะเป็นแบบธรรมดา หรือ extended ก็ได้ครับ) ขอบคุณล่วงหน้าด้วยครับ. จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 11 ส.ค. 52 01:22:27

ความคิดเห็นที่ 43 Definition The extended real number system consists of the real field R and two symbols,-ฅ and ฅ. We preserve the original order in R and defined                 -ฅ<x<ฅ for every x in R it is clear that +ฅ is an upper bound of every subset of extended real number system. credit  : Mathmatical analysis , Walter Rudin แก้ไขเมื่อ 11 ส.ค. 52 01:34:10 แก้ไขเมื่อ 11 ส.ค. 52 01:32:29 จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 01:31:32

ความคิดเห็นที่ 44 ^ ม่ายยอมไปนอนซะที ^^ "ผมคิดว่ามันเป็นได้ทั้ง เป็น และไม่เป็น แล้วแต่ context" >>อ้อ คล้ายๆกับที่ว่าบางสำนักมองว่า1/0 = infinity ใช่ไหมคะ คือตอนนี้ ยังไม่ทำความเข้าใจร่วมกันว่าจะให้มันเป็นหรือไม่เป็น จำนวนแน่ๆ บางทีมิ้นอาจจะเข้าใจแค่สำนักเดียวแบบนี้ เมื่อกี้แวปดูความเห็นคุณลุงแว่นใจดีแล้วมีสองคำที่ติดใจ nothing กับ can be many things ให้ A x 0 = 0 A = 0/0 0/0 = can be many things ให้ B แทนอะไรที่ x0 = 1 B = 1/0 ? B = nothing --------------------------------- ไม่แน่ใจว่า ทั้ง A และ B ควรตอบว่า อะไรดี จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : 11 ส.ค. 52 01:36:42

ความคิดเห็นที่ 45 แอบปิ๊งไอเดียของคุณ nonlocality ใน #31 ^^ ผมชอบการใช้คำว่า "ไม่กำหนด" จริง ๆ แฮะ ถ้าแปลคำว่า indeterminate เป็น ไม่กำหนด ผมว่าจะฟังดูเข้าท่า และใกล้เคียงกับคำในภาษาอังกฤษที่สุด เพราะมันใช้ได้ตั้งแต่ ในแง่ที่ว่า ไม่(สามารถ)กำหนด(ค่า)ได้, ยังไม่ได้กำหนด, ไม่ยอมกำหนด, กำหนดไม่ได้ ฯลฯ เทียบเคียงความหมายกับคำเดิมในภาษาอังกฤษ ได้ดีกว่าคำว่า "หาค่าไม่ได้" (ซึ่งชวนให้นึกถึง invaluable, priceless, หรือ worthless) มากครับ. จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 11 ส.ค. 52 01:36:44

ความคิดเห็นที่ 46 #44 ก่อนที่เราจะตอบว่ามันคืออะไรดี เราต้องตอบคำถามพวกนี้ก่อนครับ ให้ A x 0 = 0 A = 0/0 ---------------------------------------------------------------- ทำไม A =0/0 บรรทัดนี้มาได้อย่างไร ห้ามตอบว่าหารด้วย 0 หรือ ย้าย 0 มาหารนะครับ เพราะการหารด้วยศูนย์ undefined --------------------------------------------------------------- 0/0 = can be many things ---------------------------------------------------------------------- ให้ B แทนอะไรที่ x0 = 1 B = 1/0 ? B = nothing ---------------------------------------------------------------- ด้วยคำถามเดียวกันจากข้างบน ปล.ยังไม่นอนครับคือนี้อาจจะไม่ได้นอน ทำการบ้านส่งพรุ่งนี้ ดองมานาน 55555 มากำลังผ่อนคลายตอบปัญหาเบา ๆ แก้ไขเมื่อ 11 ส.ค. 52 01:44:12 จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 01:43:09

ความคิดเห็นที่ 47 #45 จริงแล้ว indeterminate form ศัพท์ไทยใช้คำว่า รูปแบบไม่กำหนดนะครับ จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 01:47:37

ความคิดเห็นที่ 48 ขอบคุณ Mr. Fusion คห 33 ที่เข้ามาทำให้ผมตาสว่างขึ้น ขออธิบายเพิ่มเติม ใน คห ของผม (คห 30) คำว่า ปัญหาทางกายภาพที่ผมกล่าวถึง ผมแปลจากภาษาอังกฤษ ของคำว่า physical problem ในความคิดของผม ปัญหาทางกายภาพ หรือ ปัญหาทางฟิสิกส์ ที่ผมสนใจอยู่ ค่าตัวเลขต่าง ๆ ที่คำนวณได้ หรือ วัดได้มีความละเอียดไม่เท่ากับอนันต์ (ความละเอียดในการวัด ขึ้นกับ เทคโนโลยีที่ใช้ แต่อย่างไรก็ไม่มีทางเท่ากับอนันต์แน่นอน) ขอยกตัวอย่างหนึ่ง (ตาม คุณศล ใน คห 39) แม้ว่าในทางคณิตศาสตร์ เราจะบอกว่า ด้านตรงข้ามสามเหลี่ยมมุมฉากที่มีความยาวด้านประกอบมุมฉากทั้งสองด้านเท่ากับ 1 จะมีความยาวด้านตรงข้ามมุมฉากเท่ากับ sqrt(2) ซึ่งเป็นจำนวนอตรรกยะ แต่ในความเป็นจริงเราไม่สามารถทำการวัดค่านี้ที่ความละเอียดเท่ากับอนันต์ได้ ดังนั้นค่าที่วัดจริง จะเป็นจำนวนตรรกยะ เท่านั้น เมื่อผมคิดเช่นนี้ ผมจึงบอกว่า อนันต์ เป็นสิ่งสมมุติขึ้น ไม่มีจริง ขอขอบคุณความเห็นของทุกท่าน และ ขอยอบรับทุกความเห็นที่แตกต่าง ปล. ผมอ่อนภาษาอังกฤษมาก และ ไม่ได้เรียนทางด้านคณิตศาสตร์มา ดังนั้น หากผิดพลาดประการใด ช่วยชี้แนะด้วยครับ แก้ไขเพิ่มเติม ปล. แก้ไขเมื่อ 11 ส.ค. 52 03:24:19 แก้ไขเมื่อ 11 ส.ค. 52 01:59:16 จากคุณ : nonlocality เขียนเมื่อ : 11 ส.ค. 52 01:49:30

ความคิดเห็นที่ 49 #46 อ๊าา เจอแบบนี้ก็ไม่รู้จะตอบว่ายังไงเลยค่ะ งั้นลองปรับเวลาขึ้นไปสมัยเพิ่งมีจำนวนใหม่ๆ ก่อนที่ยังไม่ได้บอกว่า การหารด้วย 0 นั้น undefined ถ้าไม่ให้ปรับนาฬิกา ก็จะลบสองบรรทัดนั้นทิ้งไปเลยเป็น ให้ A x 0 = 0 A = can be many things? ให้ B x0 = 1 B = nothing? แบบนี้ถูกไหมคะ หากจะถามหาค่าของ A,B ควรตอบว่าอย่างไรดี? จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : 11 ส.ค. 52 01:49:55

ความคิดเห็นที่ 50 #48 เข้าใจความคิดคุณ nonlocality แล้วครับ พอบอกว่าหมายถึง physical problem เรื่องนี้ชวนในนึกถึงนักคณิตศาสตร์ท่านหนึ่ง ที่บอกว่าเขาสามารถตัดกระดาษสี่เหลี่ยมเป็นชิ้นย่อย ๆ แล้วเอามาต่อกันได้ใหม่เป็นวงกลมสมบูรณ์ (จำไม่ได้แล้วว่ากี่ชิ้น แต่คิดว่าเป็นหลักแสน) แต่ trick ของท่าน (ไม่แน่ใจว่าผมเข้าใจท่านถูกหรือเปล่า) คือ ต้องใช้กรรไกรที่สามารถตัดแบบ recursive ได้ (รอยตัดมันจะดูเป็นรูปร่าง คล้าย ๆ fractals ครับ) #44,#49 ผมคิดว่าคนส่วนใหญ่ (ที่อย่างน้อยก็ต้องเรียนคณิตศาสตร์ ตั้งแต่เล็ก) น่าจะตอบคำถาม 0/0 = ? ว่า undefined ครับ ซึ่งเหตุผลหนึ่งก็เพราะว่ามัน can be many things เหมือนในตย. A นั่นแหละครับ แต่ทั้งนี้ จะใช้คำว่า indeterminate ก็ได้เช่นกันครับ ส่วนข้อ B นั้น ผมว่า There is nothing but infinity that can be your B (i.e. something that multiplied by 0 and has the result = 1). But even infinity cannot be B, since if B is infinity, then what is C, given C is something multiplied by 0 and has the result = 2? ประมาณนี้มั้งครับ ;-) ปล. เลยยังไม่ได้ไปนอนเลย - -" (<-- ^^) จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : 11 ส.ค. 52 01:57:22

ความคิดเห็นที่ 51 โจทย์ของคุณ nonlocality  น่าสนใจดีค่ะ infinity กับความริง ขอร่วมคิดด้วยคนค่ะ แม้ว่า มวลของจักรวาล หรือขนาดอาจจะไม่ใช่ infinity งั้น 1.ถ้าเป็นเงาสะท้อน ในกระจกสองบานที่วางขนานกัน จะบ่งบอกถึงความเป็น infinity ได้ไหมคะ ------------------------------------------------------------ #50 ชอบบรรยากาศแบบนี้จังเลย แต่ไม่ไหวแล้วพรุ่งนี้มีเรียน ขอบคุณทุกๆคนมากๆค่ะ ราตรีสวัสดิ์ จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : 11 ส.ค. 52 02:05:45

ความคิดเห็นที่ 52   lim       (sin x)     =   ?    ครับ n-->inf   --------                n จากคุณ : ONaja เขียนเมื่อ : 11 ส.ค. 52 02:28:55

ความคิดเห็นที่ 53   ตอบ 6 ครับ จากคุณ : ONaja เขียนเมื่อ : 11 ส.ค. 52 02:29:34

ความคิดเห็นที่ 54 ขอตอบคุณ mint_la (คห 51) ตามความเห็นของผมนะครับ (ใครว่ามั่วก็ยอม) ในความเป็นจริง (คือ ถ้าคุณทำการทดลองนับจำนวนเงาสะท้อนจริง ๆ) คุณจะไม่สามารถนับจำนวนเงาสะท้อนในกระจกสองบาน ที่วางขนานกันได้ อย่างไม่มีที่สิ้นสุด ไม่ใช่เพราะคุณเหนื่อยแล้วจะนับไม่ไหวนะครับ แต่เพราะในโลกนี้ ไม่มีกระจกที่สมบูรณ์ที่สามารถสะท้อนแสงได้ 100% ดังนั้นทุกภาพที่เกิดจากการสะท้อนแต่ละครั้ง จะเกิดการสูญเสียแสงไป (เนื่องจาก การกระเจิงที่ผิว การดูดกลืนแสง หรือ ด้วยเหตุอื่น ๆ) ถึงแม้ว่า การสูญเสียนี้จะน้อยมากสำหรับกระจกที่ค่อนข้างสมบูรณ์ แต่การสูญเสียนี้ก็ยังมีอยู่ ดังนั้นเมื่อคุณนับไปถึง จำนวนภาพที่สะท้อนมาก ๆ (น่าจะอยู่ที่หลักหมื่น สำหรับกระจกดี ๆ) ผลกระทบจากความไม่สมบูรณ์ของกระจกนี้ จะทำให้คุณนับต่อไปไม่ได้ ดังนั้น สำหรับผมคำว่า อนันต์ จึงเป็นสิ่งที่ไม่มีจริงในปัญหาทางกายภาพ แต่ในชีวิตประจำวัน หากคุณเอากระจกสองอันมาวางขนานกัน แล้วเห็นภาพสะท้อนมากกว่าร้อยภาพ คุณก็อาจบอกว่ามันสะท้อนอนันต์ครั้งแล้ว (โดยอ้างอิง จากสูตรทางคณิตศาสตร์ ที่ละเลยความไม่สมบูรณ์ของกระจก) แก้ไขเมื่อ 11 ส.ค. 52 02:39:41 จากคุณ : nonlocality เขียนเมื่อ : 11 ส.ค. 52 02:29:57

ความคิดเห็นที่ 55 ให้ A x 0 = 0 A = can be many things ให้ B x0 = 1 B = nothing ถ้ายอมรับสิ่งนี้ มันก็ยังไม่มีอะไรบ่งบอกว่า A = 0/0 B = 1/0 #50 ทำไม 0/0 ถึง can be many things ถึง Ax0 = 0 , A can be many things แต่เราจะให้เหตุผลอย่างไรว่า A = 0/0 สมมติว่าการหารด้วยศูนย์ทำได้ Ax0/0 = 0/0 ต้องแสดงให้ได้ว่า Ax0/0 = A จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 02:39:03

ความคิดเห็นที่ 56 #54 ประเด็นตรงนี้คือ ความจริงทางคณิตศาสตร์ กับ ความจริงทางวิทยาศาสตร์กายภาพ แตกต่างกัน ความจริงทางคณิตศาตร์ไม่สามารถรับรู้ หรือ ค้นพบผ่านประสาท สัมผัสผ่านทางการได้ยิน การเห็น การรับกลิ่น การลิ้มรส การสัมผัส เพราะฉะนั้นการมีอยู่ของ infinity ไม่สามารถรับรู้ได้ด้วยการมองเห็น แต่ประสาทสัมผัสนั้นจำเป็นสำหรับการนำยังความจริง ถ้าจะถกแบบวิทยาศาสตร์ กับ คณิตศาสตร์น่าจะคุยกันไม่รู้เรื่อง เพราะปรัชญามันค่อนข้างแตกต่าง จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 02:51:40

ความคิดเห็นที่ 57 ในเรื่องของอนันต์ ผมเคยได้ยินมาว่า การที่เราจะเดินทางจากจุดหนึ่งไปอีกจุดหนึ่งนั้น ต้องผ่านครึ่งหนึ่งของระยะทาง ครึ่งของครึ่งของระยะทาง ครึ่งของครึ่งของครึ่งของระยะทาง  ครึ่งของๆๆๆระยะทาง แล้วก็ครึ่งของๆๆๆไปเรื่อยๆ อ้าวถ้าอย่างนั้นเราก็เดินทางเป็นอนันต์เลยซิ แก้ไขเมื่อ 11 ส.ค. 52 02:55:37 จากคุณ : ทะเลคราม (blueocynia) เขียนเมื่อ : 11 ส.ค. 52 02:54:57

ความคิดเห็นที่ 58 ขอบคุณคุณ เซียนแห่งmath (คห 56) และ คุณ blueocynia (คห 57) ที่ชี้ทาง เมื่อพิจารณาแล้ว ผมคิดว่า ผมผิดเองที่กล่าว เชื่อมโยง ค่าอนันต์ กับ ปัญหาทางกายภาพ (ใน คห ที่ 30) ดังนั้น ก็ขออภัยทุกท่าน โดยเฉพาะ ลุงแว่นใจดี ที่เบี่ยงประเด็น ของกระทู้นี้ ขอเชิญชวน ทุกท่าน คุยกับต่อ ในหัวข้อของกระทู้นี้นะครับ ส่วนผม ขอนั่งอ่านเงียบ ๆ ก็แล้วกันนะครับ จากคุณ : nonlocality เขียนเมื่อ : 11 ส.ค. 52 03:10:45

ความคิดเห็นที่ 59 #52 เป็นตัวอย่างที่ดีครับ แต่ขอเปลี่ยนเป็น  sinx / x  เมื่อ x เข้าใกล้ 0 จะได้ว่า  sin(0)/0 = 0/0  , can be any things จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 03:12:30

ความคิดเห็นที่ 60 ชอบกระทูเแบบนี้จัง อยากอ่านต่อแต่ต้องขับรถไปธุระแต่เช้า เดี๋ยวแหกโค้ง +3+ ไปละครับ แก้ไขเมื่อ 11 ส.ค. 52 03:17:23 จากคุณ : End of Love เขียนเมื่อ : 11 ส.ค. 52 03:14:55

ความคิดเห็นที่ 61 #57 ปัญหาอันนี้คล้ายกับที่ผมเคยสอนเด็ก ถ้าเรามีวงกลมอยู่ 1 วง เราระบายสีครึ่งนึง แล้วระบายสีอีกครึ่งนึงของที่ยัง ไม่ได้ระบาย แล้วระบายอีกครึ่งนึงของที่ยังไม่ได้ระบาย ถ้าเรามีดินสอวิเศษเราจะระบายสีได้เต็มวงหรือไม่ เด็กตอบว่า ไม่เต็มเพราะเราแบ่งครึ่งมันจะมีครึ่งที่เหลืออยู่เสมอที่เรา ไม่ได้ระบาย ผมจึงบอกเด็กไปว่าเดี่ยวเรียนไปอีกหน่อยสัก มปลาย เราจะรู้ว่า ถ้าสีนั้น เป็นสีที่วิเศษจริง เราจะระบายได้เต็มวง จากคุณ : เซียนแห่งmath เขียนเมื่อ : 11 ส.ค. 52 03:19:49

ความคิดเห็นที่ 62 #57 Zeno 's Paradox? นึกเรื่องนี้แล้วผมนึกถึง fractal แหะ จะว่าไป fractal นี่ก็ความยาวเป็นอนันต์เหมือนกันใช่รึเปล่าครับ? จากคุณ : house (panote_saechiew) เขียนเมื่อ : 11 ส.ค. 52 09:48:32

ความคิดเห็นที่ 63 สวัสดีครับคุณลุงแว่นใจดี ผมเรื่อย ๆ ไม่สุขไม่ทุกข์อะไรมากครับ คุณลุงแว่นสบายดีนะครับ? (คิดถึงครับ) ผมชอบอ่านที่ คุณลุงแว่นใจดี คุยกับ คุณเซียนแห่งmath ครับ แต่กิฟไม่พอแจกให้ 2 ท่าน ทั้ง 2 ท่านได้ใจไปเต็ม ๆ เลยนะครับ #62 คุณ panote_saechiew fractal ที่มีความยาวเป็น 0 ก็มีครับ cantor dust ไง :P (ถึงแม้มันจะมีความยาวเป็น 0 แต่มันก็มีจำนวนสมาชิกเยอะกว่าเซ็ตจำนวนเต็ม! - อนันต์ที่ใหญ่กว่าอนันต์) จากคุณ : ศล เขียนเมื่อ : 11 ส.ค. 52 09:55:53

ความคิดเห็นที่ 64 กระทู้ดี ต้องโหวตตตต จากคุณ : KinkyVans เขียนเมื่อ : 11 ส.ค. 52 11:05:09

ความคิดเห็นที่ 65 57# อนันต์มันเป็นแค่นิยามที่เราสรัางขึ้นมาสำหรับสิ่งที่มีจำนวนไม่จำกัด ความเป็นจริงแล้ว ความยาวไม่มีอนันต์ มันมีแต่ความต่อเนื่องของอวกาศและเวลา ถ้าเราแบ่งความต่อเนื่อง ออกเป็นหน่วยย่อยๆตามที่มนุษย์เราชอบทำกัน เราก็จะแบ่งได้เป็นอนันต์หน่วย (อย่าลืมว่า Mathematic model ของมนุษย์ยังมีพื้นฐานบนความเท่ากันของหน่วยย่อย มันมีกรณีที่แต่ละหน่วยไม่เท่ากันด้วย เช่น จาก 0 ถึง 1 มีความยาวไม่เท่ากับ 1 ถึง 2) ฉะนั้น ผมจึงไม่ค่อยรู้สึกตื่นเต้นอะไรกับโลกแ่ห่งความไม่จำกัด ไม่ใช่เพราะความเป็นจริง ทุกอย่างมันจำกัด แต่เพราะความเป็นจริงมันมีแค่การต่อเนื่องกับไม่ต่อเนื่อง สิ่งที่ต่อเนื่องได้แก่ อวกาศและเวลา ส่วนสิ่งที่ไม่ต่อเนื่องก็ได้แก่ อนุภาค สสาร จากคุณ : P.Virie เขียนเมื่อ : 11 ส.ค. 52 11:10:23

ความคิดเห็นที่ 66 ถ้าไม่ได้อ่านกระทู้นี่ หากมีคนมาถามผมว่า 0/0 ได้เท่าไหร่ ผมคงตอบว่าจะบ้าเหรอ จะหารไปทำไม ขอบคุณที่ทำให้กรอบความคิดของผมกว้างขึ้นครับ จากคุณ : aladin_71 เขียนเมื่อ : 11 ส.ค. 52 12:00:22

ความคิดเห็นที่ 67 แฟนคลับมาแล้วค่ะ ^^ จากคุณ : Choco-Mix เขียนเมื่อ : 11 ส.ค. 52 12:06:29

ความคิดเห็นที่ 68 แปลกแต่จริง เราสร้างเส้นยาว (2)1/2 หน่วย ได้ แต่เรากลับบอกความละเอียดทุกรายละเอียดของ  (2)1/2 ไม่ได้ ปล. ไม่แม่นพื้นฐานทางด้านคณิตศาสตร์ จึงได้แต่มองห่างๆ T-T จากคุณ : jesus_god เขียนเมื่อ : 11 ส.ค. 52 12:31:58

ความคิดเห็นที่ 69 ปวดสมองเลยเห็นทู้นี้ จากคุณ : DEKOP เขียนเมื่อ : 11 ส.ค. 52 13:11:34

ความคิดเห็นที่ 70   ค.ห. 52   ตอบ 6 เพราะว่าแบบนี้ครับ   lim       (sin x)        lim     (six)          ,   n ตัด n   (ฮา) n-->inf   -------   = n-->inf                n                         =   lim   6      =    6                            n-->inf เป็นมุขของอาจารย์ผม วิชาการมากไปปวดหัวนะครับ ผ่อนคลายหน่อย อิอิ จากคุณ : ONaja เขียนเมื่อ : 11 ส.ค. 52 13:25:17

ความคิดเห็นที่ 71 อนันต์นั้นไม่ใช่ตัวเลข มันเป็นเพียงสิ่งที่เราเขียนแทนจำนวนที่มีค่ามากจนไม่อาจเขียนในรูปอื่นได้ ตัวอย่างค่าอนันต์ที่มีในธรรมชาติ เช่น ค่า p หรือ e ซึ่งเป็นจำนวนที่นักวิทยาศาสตร์ยอมรับว่ามีอยู่จริง มีความหมาย และเป็นองค์ประกอบของหลายๆสิ่งบนโลก แต่จนถึงบัดนี้ เราก็ยังหาทศนิยมตำแหน่งสุดท้ายไม่ได้ (เหมือนจะมีการพิสูจน์ไปแล้วด้วยว่า p นั้นมีทศนิยมเป็นอนันต์จริงๆ) ดังนั้นใครที่ว่าค่าอนันต์ไม่มีความหมายนั้นผมเถียงครับ แต่คำถามคือ ทำไมเราต้องไปสนใจค่าอนันต์ ทั้งๆที่มันไม่ค่อยจะมีความหมายอะไรในชีวิตประจำวันเลย คนอื่นว่าไงไม่ทราบ แต่สำหรับผม ผมเห็นว่ามันเป็นความสวยงามอย่างหนึ่งในธรรมชาติ ปล. ว่าแต่ตกลง 00 เนี่ยมันเท่ากับเท่าไหร่ ผมเคยคิดว่ามันไม่นิยามเพราะมีความหมายเท่ากับ 0/0 จากคุณ : unholy เขียนเมื่อ : 11 ส.ค. 52 13:30:26

ความคิดเห็นที่ 72   ขอบคุณ ลุงแว่นใจดี ครับ ถ้าหากจำได้ สำหรับคำแนะนำดี ๆ เกี่ยวกับ Algorithm ครับ จากคุณ : ONaja เขียนเมื่อ : 11 ส.ค. 52 13:34:23

ความคิดเห็นที่ 73   ตอบ ค.ห. 71  0 ยกกำลัง 0 ได้ 1 ครับ (โดยใช้ lim) แก้ไขเมื่อ 11 ส.ค. 52 13:41:12 จากคุณ : ONaja เขียนเมื่อ : 11 ส.ค. 52 13:36:40

ความคิดเห็นที่ 74 71# อนันต์ไม่มีในธรรมชาติครับ ในความเห็นของผม มันคือความต่อเนื่อง แต่มนุษย์พยายามนับมัน เลยได้อนันต์ออกมา จากคุณ : P.Virie เขียนเมื่อ : 11 ส.ค. 52 13:44:59

ความคิดเห็นที่ 75 นี่แหละหว้ากอ!! จากคุณ : Disorder เขียนเมื่อ : 11 ส.ค. 52 14:29:29

ความคิดเห็นที่ 76 ขอบคุณค่ะ ความรู้อัดแน่นจริง (มองตาปริบๆ อ่านอย่างเดียวเลย ;P) จากคุณ : pongpei เขียนเมื่อ : 11 ส.ค. 52 15:02:35

ความคิดเห็นที่ 77 #74 คุณ P.Virie (ความเห็นส่วนตัว) ผมคิดว่าอนันต์กับความต่อเนื่องในกรณีที่พูดถึงนั้นเป็นอย่างเดียวกันนะครับ อยู่ที่ว่าเราจะใช้คำว่าอะไรและมองมันแง่ไหนเท่านั้นเอง ถ้าเราจะอธิบายว่ามันต่อเนื่อง ตอนที่ถูกถามว่าทำไมต่อเนื่อง เราจะอธิบายยังไงครับถ้าไม่ใช้ concept ของอนันต์ ทำนองเดียวกัน เราจะบอกได้ไงครับว่าสิ่งนี้อนันต์ ถ้ามันขาด concept ของความต่อเนื่อง ทั้งความคิดเรื่องความต่อเนื่องและอนันต์ (ในกรณีที่พูดถึงนี้) ผมคิดว่าถ้าอันใดอันหนึ่งมีในธรรมชาติ อีกอันก็จะต้องมีในธรรมชาติด้วย (เพราะสะท้อนคุณลักษณะอย่างเดียวกันครับ) - แต่มันจะมีในธรรมชาติ (nature) จริง ๆ หรือเปล่า ยังไม่พูดถึงครับ จากคุณ : ศล เขียนเมื่อ : 11 ส.ค. 52 16:12:43

ความคิดเห็นที่ 78 77# "ตอนที่ถูกถามว่าทำไมต่อเนื่อง เราจะอธิบายยังไงครับถ้าไม่ใช้ concept ของอนันต์" เหมือนคำถามที่ว่า ทำไมมวลถึงมีปฏิกิริยาต่อแรง ผมก็คงอธิบายไม่ถูกเหมือนกับครับ เพราะว่าคนเราคิดคำว่าอนันต์จนมันเป็น Axiom ในหัวไปซะแล้ว (เช่นเดียวกับที่ คนเรารู้่ว่าออกแรงให้มวล มันย่อมเคลื่อนที่)  แต่ผมเชื่ออย่างสุดใจว่า อนันต์มันเกิดมาจากการที่คนเราพยายามนิยามความต่อเนื่อง จากคุณ : P.Virie เขียนเมื่อ : 11 ส.ค. 52 16:20:46

ความคิดเห็นที่ 79 แล้วถ้าเป็นอย่างนี้หละ 1/0+1/0 = 2/0 1/0-1/0 = 0/0 = 0^0 <> 0^1    ************ 1/0*1/0=1/(0*0) 0^n <> 0               ************ 1 / (1/0) = 0 1 / (2/0) = (1/2)0 0*n <> 0                ************ 1-1=0 (1-1)*0=0^2 (1-1)*0/(0^2)=(0/0)^2 0*(1/0) =1 0*(2/0) =2 (0/0)*1=1 (0/0)*2=2 (0/0)=1 0*6>0*5 มึนนะนี่ อันนี้ นิยาม 0 มากกว่า 0 ในนิยามเดิม และคงจะได้ inf น้อยกว่า inf ในนิยามเดิมเหมือนกัน จากคุณ : aLITTLEspaceAround7day เขียนเมื่อ : 11 ส.ค. 52 16:33:29

ความคิดเห็นที่ 80 ในความเห็นผม อนันต์มีในธรรมชาติจริงแน่ๆครับ ตัวอย่างเช่น ความคิดของมนุษย์ที่เป็นนามธรรมนี่แหละ(ทั้งอภิปรัชญาและคณิตศาสตร์) สามารถคิดไปได้เรื่อยๆไม่สิ้นสุดเป็นอนันต์ ลองพิจารณาได้จาก Godel's incompleteness theorems ครับ http://en.wikipedia.org/wiki/G%C3%B6del%27s_incompleteness_theorems Stephen Hawking เมื่อพิจารณาทฤษฎีบทนี้ ยังถึงกับเคยกล่าวไว้ว่าทฤษฎีแห่งสรรพสิ่ง คงจะหาเอาด้วย"ความคิด"ไม่ได้เสียแล้ว เพราะมันคงไม่จบไม่สิ้น Stephen Hawking was originally a believer in the Theory of Everything but, after considering Godel's Theorem, concluded that one was not obtainable. “ Some people will be very disappointed if there is not an ultimate theory, that can be formulated as a finite number of principles. I used to belong to that camp, but I have changed my mind. แก้ไขเมื่อ 11 ส.ค. 52 18:09:42 แก้ไขเมื่อ 11 ส.ค. 52 18:07:22 จากคุณ : EvaAngelion เขียนเมื่อ : 11 ส.ค. 52 18:04:31

ความคิดเห็นที่ 81 กระทู้นี้ ทำให้หว้ากอ กลับมาเป็นหว้ากออีกครั้ง หลังจากรอนแรมในทะเลมานาน กับเรื่องลึกลับ และ เรื่องทหาร โหวตครับ จากคุณ : Mikoyan เขียนเมื่อ : 11 ส.ค. 52 18:27:29

ความคิดเห็นที่ 82 เข้ามาในกระทู้รู้สึกว่าผมจะเหมือนกับมิซึฮาระ คานะ ที่กำลังฟังบรรยายของตาโทมะ โซ ในเรื่องQ.E.D.เลย = =" จากคุณ : ไทยวรรษ สีทันดรสมุทร (spiralhead) เขียนเมื่อ : 11 ส.ค. 52 19:18:32

ความคิดเห็นที่ 83 ความเห็นส่วนตัวของผมต่อไปนี้อาจจะสวนกระแสนิดนึง แต่อยากให้ลองอ่านกันดูครับ เห็นกระทู้เกี่ยวกับ infinity และ หารด้วย 0 อยู่บ่อยๆ มานานแล้ว ผมรู้สึกแปลกใจและอึดอัดใจนิดหน่อย ที่หลายคนเขียน 1/0, a/0, 1/infinity กันโดยไม่รู้สึกอะไร เสมือนมันเป็นตัวเลขธรรมดาๆตัวหนึ่ง เค้าจะรู้หรือปล่าวว่าสิ่งที่เค้าเขียนลงไปนั้น เค้าหมายความว่าไง... อันดับแรกเลย "/" จริงๆแล้วไม่มีความหมายหากไม่ได้อยู่ใน context ของ field ใน field ใดๆ เรามี binary operations แค่ 2 ตัวเท่านั้นคือ + และ * http://en.wikipedia.org/wiki/Field_%28mathematics%29 a/b เป็นแค่ notation หมายถึง a*b^(-1)  โดยที่ b^(-1) หมายถึงอินเวอร์สการคูณของ b (เราอาจจะมองเป็น unary operation ใน field ก็ได้) เนื่องจาก 0 ไม่มีอินเวอร์สการคูณ การเขียน 1/0, 2/0 etc มันไม่มีความหมาย ไม่ make sense ทำนองเดียวกัน การเขียน 1/infinity ก็ไม่มีความหมาย ทำไมถึงไม่มีความหมาย? ก็เพราะอย่างที่บอกไป "/" เป็น notation ที่มาจาก operations * และ ^(-1) ใน filed แต่ infinity ไม่ใช่สมาชิกใน field การเขียนแบบนั้นจึงไม่ make sense บางคนอาจจะแย้งว่า infinity เป็นสมาชิกใน extended real numbers แต่อยากจะบอกว่า extended real numbers ไม่ใช่ field นะครับ มันเป็นแค่การเอา +inf, -inf มาเติมใน real numbers แล้ว "นิยาม" algebraic  operations ที่เกี่ยวข้องกับสองสมาชิกใหม่แบบคร่าวๆ เท่านั้น มันไม่ใช่ formal mathematical stucture ครับ  http://en.wikipedia.org/wiki/Extended_real_number_line#Algebraic_properties Intermediate form ที่เราเห็นกันนั้น เป็น expression ใน context ของ limit ทั้งสิ้น ในวิกิเขียนไว้ชัดเจน: "An indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution does not give enough information to determine the original limit, it is known as an indeterminate form." http://en.wikipedia.org/wiki/Indeterminate_form ใน context ของ limit เราอาจจะเขียน 1/0, 1/inf ได้ ตราบใดที่เราระลึกอยู่เสมอว่ากำลังอยู่ใน context ของ limit ความหมายของมันคือ limit_{x->0} 1/x, limit_{x->inf} 1/x ตามลำดับ 1/0 ไม่ได้อ่านว่า หนึ่งส่วนศูนย์ แต่ควรอ่านว่า ลิมิตในรูปของหนึ่งส่วนศูนย์  เพื่อเตือนตัวเองว่ากำลังอยู่ใน context ของ limit นะ เรื่อง infinity ก็เหมือนกันครับ infinity ไม่ใช่จำนวน เป็น concept ของ limit  เป็นผลลัพธ์ที่เกิดขึ้น จากกระบวนการของ limit เห็นสัญลักษณ์เลข 8 นอน ที่ไหน ให้ทราบได้เลยว่ามีกระบวนการทาง limit เกิดขึ้น การเขียนเช่น inf + 1, inf + inf นั้น ถ้าพูดกันแบบจริงจังแล้วต้องบอกว่าไม่ถูกต้อง ไม่ make sense เหตุผลก็เหมือนที่กล่าวไปแล้ว inf ไม่ใช่จำนวน จะนำมาบวกกันได้ยังไง เครื่องหมาย "+" ใน "inf + inf" หมายถึงอะไรเหรอครับ ผมไม่เข้าใจความหมาย หมายถึงการบวกกันอย่างที่เราๆเข้าใจหรือปล่าว ถ้าใช่ แล้วเราจะบวกกันยังไง ในเมื่อเราไม่รู้ว่า inf มันคืออะไร มันเป็นสิ่งแปลกปลอมในระบบจำนวน Infinity is a concept of limitting process. A real number + a concept = ???   A real number divided by a concept = ??? อืมม ที่ผมเขียนมาซะยาวนี่เป้าหมายไม่ได้ต้องการสวนกระแส หรืออะไรนะครับ การคุยกัน ถกกันเป็นเรื่องที่ดี ผมแค่อยากให้ระวังกันนิดนึง ผมทราบดีว่าหลายท่านในนี้ทราบดีแก่ใจ ว่าการเขียน 1/0 หมายถึงอะไร แต่ยังมีอีกหลายท่านที่นึกว่า 1/0 เป็น algebraic expression ธรรมดา ไม่เกี่ยวกับ limit ทำให้เป็นตัวอย่างที่ผิดๆให้เยาวชนที่ผ่านมาอ่าน เข้าใจผิดว่า "เออ เขียน 1/0, inf + 1 ได้ด้วยแฮะ เอาไปเขียนเป็นคำตอบการบ้านส่งครูมั่งดีกว่า" จากคุณ : packham เขียนเมื่อ : 11 ส.ค. 52 19:44:03

ความคิดเห็นที่ 84 /me เข้ามาเหมือน คคห. 82 จากคุณ : Shinjitsu เขียนเมื่อ : 11 ส.ค. 52 19:46:06

ความคิดเห็นที่ 85 80# ผมว่าพวกนักวิทยาศาสตร์ดังๆ แค่พูดออกมาเพื่อเสริมศรัทธาในตัวเองครับ ในทางนามธรรม อะไร อะไรก็ Unlimited ได้ แต่ถ้าพูดกันจริงๆแล้ว ความคิดคนเรามันจะอยู่ได้นานเกินกาลปวสานของเผ่าพันธุ์มนุษย์หรือไม่ ต่อให้มี extraterrestrial life มาสานต่อ มันก็ึคงยุติที่จุดจบของเวลาและอวกาศ หรือไม่ก็เมื่อตอนที่ Entropy ของจักรวาลมันกระจายตัวเต็มที่แล้วครับ 83# ชัดเจนดีครับ แต่ไม่ได้สวนกระแสเลย หลายคนในนี้ก็ให้ความเห็นคล้อยตามครับ จากคุณ : P.Virie เขียนเมื่อ : 11 ส.ค. 52 20:11:41

ความคิดเห็นที่ 86 กระทู้เจ๋งดี แต่ใช้เวลาอ่านนานมากค่ะ เพราะต้องเปิดดิกไปด้วย แหะๆ จากคุณ : มือปราบหน้าใส เขียนเมื่อ : 11 ส.ค. 52 20:42:43

ความคิดเห็นที่ 87 เข้ามาลงชื่อไว้ก่อน เดี๋ยวกลับมาอ่านใหม่ ท่าทางกระทู้นี้ต้องใช้เวลา(คิด)นานหน่อย จากคุณ : samapapa เขียนเมื่อ : 11 ส.ค. 52 21:12:49

ความคิดเห็นที่ 88 #83 คุณ packham ส่วนใหญ่เห็นด้วยนะครับ แต่มีบางส่วนที่ไม่เข้าใจครับ (ส่วนนี้จะบอกว่าไม่เห็นด้วยก็ไม่ได้) และก็คิดว่าไม่ได้สวนกระแส (เอาเข้าจริง อาจไม่มีใครคิดว่า 1/0 คือ 1 หารด้วย 0 ด้วยซ้ำครับ - ถึงแม้อาจจะมีบางคนลืมคิดไปว่าอินเวิร์สการคูณของ 0 ไม่มี) 1. ตกลง 1/0 หรือ 1/ฅ เป็น indeterminate form หรือครับ หรือผมอ่านที่คุณเขียนแล้วจับความผิด (แหะ ๆ ถ้าเป็นเคสจับความผิดขออภัยครับ) 2. จำเป็นเสมอรึเปล่าครับที่เราเห็น 1/ฅ แล้วต้องนึกว่ามันอยู่ใน context ของลิมิต ไม่สามารถ ทำกับมันอย่างที่มันเป็นจำนวนได้? ถึงแม้ว่าทั้งนิวตันและไลบ์นิซไม่ได้เขียน 1/ฅ ออกมาตรง ๆ แต่ผมเข้าใจว่าเขาก็มี concept ของ object ที่น้อยมาก ๆ ๆ ๆ ๆ (Infinitesimal) แถมยังทำกับ object ตัวนี้แบบที่ทำกับจำนวนอีก (จำนวนจริงที่คูณกับ infinitesimal ก็ยังเป็น infinitesimal) ที่แน่ ๆ คือยังไม่มีการพัฒนาทฤษฎีลิมิตในตอนนั้น (จริงอยู่ครับว่าเราอาจบอกว่า Infinitesimal ตัวมันเองก็บ่งชี้ลิมิต - อย่างน้อยก็จากชื่อมันล่ะ 'ตำแหน่งที่อนันต์ในอนุกรม') แต่จำเป็นหรือครับ? จากคุณ : ศล เขียนเมื่อ : 11 ส.ค. 52 21:19:11

ความคิดเห็นที่ 89 ขอพารา 2 ถ้วยพูนๆ จากคุณ : La Gioconda เขียนเมื่อ : 11 ส.ค. 52 22:04:26

ความคิดเห็นที่ 90 ตอบ #54 คุณ nonlocality อื้มพอมาคิดแล้วเป็นแบบนั้นจริงๆด้วยค่ะ ลืมไปเลย สงสัยจะไม่มีแล้วมั้ง ขอบคุณสำหรับคำอธิบายค่ะ ตอบ #55 คุณเซียนแห่ง math "มันก็ยังไม่มีอะไรบ่งบอกว่า A = 0/0 B = 1/0" > อื้ม งั้นลองใหม่ค่ะ Ax0 = 0 A = can be many things A = can be (0/0) 0/0 = can be many things มั่วนะ รอคุณลุงแว่นใจดีมาเฉลยละกันค่ะ ตอบ #83 คุณ packhamผู้รู้ตัวจริง โดน ^^ เข้าใจตามนั้นค่ะ เรื่อง 0 ไม่มีอินเวิสการคูณนี้ ก็คิดว่าทุกคนคงเคยเรียนมา ขอถามคุณ packham หน่อย แบบนี้ถ้า คำตอบโผล่มา 1/0 ควรตอบว่า ไม่มีอินเวิสการคูณ ได้ไหมคะ อีกเรื่องนึง คุณลุงแว่นบอกว่า มีบางสำนักเค้านับถือว่า 1/0 = infinity ค่ะ แก้ไข เพิ่งนึกออก แก้ไขเมื่อ 11 ส.ค. 52 22:49:43 แก้ไขเมื่อ 11 ส.ค. 52 22:41:12 จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : 11 ส.ค. 52 22:25:50

ความคิดเห็นที่ 91 #88 indeterminate form ให้นึกถึงทฤษฏีของ L'hospital formใดก็ตามที่จัดอยู่ในรูปของ 0/0 หรือ ฅ/[infinity] 1/0  นั้น undefined 1/ฅ นั้นนิยามในระบบ extended นิยามจริงรู้สึกจะเป็น x/ฅ  = 0 for all x:=Real number --------------------------------------------------------------------- 1/ฅ ผมคิดว่ามันไม่มีอยู่ในโครงสร้างทางพีชคณิต คิดว่าคณิตศาตร์ในยุคนั้นยังไม่ abstract เท่าในยุคนี้ วิชา analysis น่าจะเกิดหลังแคลคูลัส ซึ่งทำให้วิชาอย่าง แคลคูลัสมีความเป็น abstract ที่รัดกุมยิ่งขึ้น การที่ limit exists ถึงไม่ใช่แค่การ take limit แต่การเป็นการที่ทุก episilon มี delta.... ########################################## #90 A = can be many things A = can be (0/0) 0/0 = can be many things ----------------------------------------------------- A = can be many things A = can be (0/0) ถ้าจะใช้สัญลักษณ์ตามคณิตศาตร์จริงนิยมเขียนแบบนี้นะครับ A := can be many things A := can be (0/0) := หมายถึงการ defined การ defined สิ่งสองสิ่งว่าเหมือนกัน ต้องอธิบายได้ว่ามันเหมือนกันอย่างไร ถ้าให้ดีต้องสามารถพิสูจน์ได้ว่ามัน equivalent กัน นิยามของ extened ที่เพิ่มเติมมาเป็น operation ของ infinity ######################################### ผมเข้าใจว่าคุณ packham จะบอกว่าจริงแล้วไม่ควรเขียน 1/0 เลยด้วยซ้ำ เพราะมันไม่มีความหมายแบบคณิตศาตร์(คำว่าไม่มีความหมายมันแปลก ๆ หมายถึงไม่defined ไม่กล่าวถึง) ถ้าจะเขียนจำเป็นต้องนึกถึงในsense ของ limit จริงแล้วควรระบุด้วย อย่างนั้นหรือเปล่า จากคุณ : เซียนแห่งmath เขียนเมื่อ : วันแม่แห่งชาติ 01:20:14

ความคิดเห็นที่ 92 ขอบคุณมากค่ะ กระจ่างแล้ว จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : วันแม่แห่งชาติ 01:30:41

ความคิดเห็นที่ 93 #91 คุณเซียนแห่งmath คำถามใน #88 ผมถามจากการพิจารณา 'ตัวบท' ของ #83 ครับ คำถามแรก มาจากการที่ผมอยากรู้ว่าย่อหน้าที่ 8-9 (บรรยาย intermediate form) ต่อเนื่องกับย่อหน้าที่ 10 (การเขียน 1/0, 1/ฅ) เป็นเหตุเป็นผลกันหรือไม่? เพราะ ย่อหน้าที่ 8-9 บอกว่า 'indeterminate form ที่เราเห็นกันนั้น เป็น expression ใน context ของ limit ทั้งสิ้น ในวิกิเขียนไว้ชัดเจน' และย่อหน้าที่ 10 บอกว่า 'ตราบใดที่เราระลึกอยู่เสมอว่ากำลังอยู่ใน context ของ limit' เพราะถ้ามีการอธิบายว่าเหตุที่เราต้องนึกถึง 1/0 หรือ 1/ฅ ใน context ของ limit เพราะ indeterminate form เป็น expression ใน context ของ limit การที่เราให้เหตุผลแบบนี้ก็หมายความว่า 1/0 กับ 1/ฅ เป็น indeterminate form ด้วยนะสิ ประเด็นของคำถามแรก ผมไม่ได้อยากรู้ว่า 1/0 กับ 1/ฅ เป็น indeterminate form รึเปล่า (หรือแม้แต่ตัวมันเป็นอะไรนะครับ) แต่อยากรู้ว่าตัวบทของ #83 ใน 3 ย่อหน้านั้นกำลังทำให้คนอ่าน อ่านแล้วเข้าใจว่า 1/0 กับ 1/ฅ เป็น indeterminate form รึเปล่าครับ (จึงเป็นเหตุผลให้ผมออกตัวว่าผมอาจจะจับความผิดตอนตั้งคำถาม) สำหรับประเด็นของคำถามที่ 2 ผมไม่ได้อยากรู้อีกเช่นกันครับว่า 1/ฅ มีหรือไม่มีความหมาย เพราะคุณ packham เองก็บอกว่ามันเป็น notation ที่เราใช้โดยระลึกถึงลิมิตของมันได้ (ย่อหน้าที่ 10) ประเด็นของคำถามนี้จึงไม่ได้พูดถึงมีอยู่หรือไม่มีอยู่ครับ แต่เป็นการถามว่ามันจำเป็นมั้ยที่เมื่อเห็น notation ดังกล่าว เราต้องนึกถึงลิมิต ถ้าเราไม่นึกถึงลิมิตแต่นึกถึง Infinitesimal ล่ะ จะเป็นยังไง? ที่คุณเซียนแห่งmath ตอบใน #91 หรือทั้งที่คุณ packham แสดงใน #83 ผมไม่มีอะไรคัดค้านเลยครับ และเข้าใจตรงตามนั้น คำถามที่ #88 ก็ไม่ได้เป็นคำถามคัดค้านครับ คำถามแรกถามถึงความสัมพันธ์ในตัวบทของ #83 คำถามที่ 2 ถามถึงความจำเป็น ว่าเมื่อเห็น 1/ฅ ต้องนึกถึงลิมิตนะ นึกถึง Infinitesimal ไม่ได้ (ผมโอเคและเชื่อว่าคำตอบคือ เพราะลิมิตรัดกุมและสอดคล้องกับระบบมากกว่า - แต่ตรงนี้ไม่ใช่สิ่งที่ผมถามนี่ครับ ผมถามว่าจำเป็นเหรอ?) - แหะ ๆ ยังไงก็ต้องขออภัยด้วยครับที่ตั้งคำถามแล้วดูนอกวงการ (นอกกระแส) ยังไงความเห็นผมทั้งหมดในกระทู้นี้ ignore ได้ครับ จากคุณ : ศล เขียนเมื่อ : วันแม่แห่งชาติ 05:28:10

ความคิดเห็นที่ 94 ตอบคุณศลใน #88, #93 นะครับ ข้อแรก 1/0, 1/inf  ไม่ใช่ indeterminate form ครับ ถึงแม้ผมจะบอกว่าอยู่ใน concept ของ limit แต่ไม่ได้ความหมายความว่า expression ที่เกี่ยวข้องกับ 0, inf ที่มาจากกระบวนการ limit ทุกตัวต้องเป็น indeterminate form หมด ถ้าสังเกตดีๆข้อความที่ผม quote มาจากวิกิ มีข้อความนี้ด้วย "does not give enough information to determine the original limit" ซึ่งเป็นส่วนสำคัญในการจำแนกว่าอันไหนใช่ indeterminate form อันไหนไม่ใช่ ยกตัวอย่างเช่น (ลิมิตในรูปของ) 0/0 มันกำกวมเพราะมันอาจมีค่าได้หลายอย่าง เช่น limit_{x->0} x^2/x = 0 หรือ lim_{x->0} sin(x)/x = 1 หรือ lim_{x->0} 3x/x = 3 เราจึงเรียก 0/0 ว่าเป็น indeterminate form ในทางตรงกันข้าม (ลิมิตในรูปของ) 1/inf นั้นเราสามารถหาค่าได้แน่นอน ไม่กำกวม คือ 0 มันจึงไม่ใช่ indeterminate form "เพราะถ้ามีการอธิบายว่าเหตุที่เราต้องนึกถึง 1/0 หรือ 1/inf ใน context ของ limit เพราะ indeterminate form เป็น expression ใน context ของ limit"  <--- ผมไม่ได้พูดหรือบอกเป็นนัยว่าอย่างนี้เลยนะครับ คาดว่าคุณ ศล คงตีความผิดไปครับ (ต้องขออภัยที่ทำให้เข้าใจผิด) ข้อสอง ผมไม่เข้าใจคำว่า infinitesimal ครับ คือผมทราบว่ามันแปลว่าอะไร แต่ไม่ทราบว่าคุณ ศลตีความว่าอย่างไร ถ้าเป็นไปได้ ช่วยให้นิยามทางคณิตศาตร์ที่ชัดเจนที่ไม่ใช่ "เล็กมากๆๆๆๆๆ" หน่อยได้ไหมครับ ผมเดาว่าต้องใช้ concept ของ limit อยู่ดี ถามว่าจำเป็นมั๊ย? ก็ไม่จำเป็นหรอกครับ เราอาจจะเขียน 1/inf และคิดว่ามันคือสิ่งที่เล็กมากๆๆๆๆ ก็ได้ แต่ก็คงได้แค่นั้น เอาไปทำอะไรต่อไม่ได้ เอาไปใช้ในบทพิสูจน์ไม่ได้ เพราะ สิ่งที่เล็กมากๆๆๆๆ เป็นภาษาพูด ไม่ใช่ภาษาคณิตศาสตร์ครับ จากคุณ : packham เขียนเมื่อ : วันแม่แห่งชาติ 09:29:08

ความคิดเห็นที่ 95 โอโฮ! แวะกลับมาแล้วพบว่า มีความเห็นเข้ามาหลากหลายมาก ๆ ผมคิดว่าน่าจะเป็นการเปิดมุมมองที่ดี และเป็นประโยชน์มากครับ ในความเห็นผม ทุกมุมมองล้วนมีประโยชน์ครับ ไม่จำเป็นว่า จะต้องคิดตามตำราเสมอไป (ไม่อย่างนั้น คงไม่มี breakthrough เกิดขึ้น) คือ เราควรสามารถตั้งคำถามได้ (แม้แต่กับตัวนิยาม/หลักเกณฑ์ต่าง ๆ ที่เราใช้กันอยู่ ก็ตาม) แล้วลองพยายามหาคำตอบ ด้วยตัวเองดู ได้ไม่ได้ยังไง ว่ากันอีกที จากนั้นจึงค่อยลองตรวจสอบ กับแหล่งอ้างอิง หรือตำรับตำราต่าง ๆ ถึงแม้ว่าจะไม่ได้พบอะไรใหม่ ๆ สำหรับส่วนรวม ก็ตาม แต่ประโยชน์อย่างหนึ่ง ก็น่าจะตกกับผู้ที่ได้ลองคิด ลองแสวงหาคำตอบ ด้วยการตั้งคำถามครับ (แต่ทั้งนี้ ควรหลีกเลี่ยงการคิดเอง เออเอง (หรือสมัยนี้เรียก มั่วนิ่ม) ด้วยนะครับ) มีมุมที่น่าสนใจเยอะมาก ๆ จะลองแจมด้วย เท่าที่พอไหวนะครับ (แบบย้อนจากคคห.ล่างขึ้นบน ก็แล้วกัน) แล้วก็จะพยายามตอบคำถามยังค้างบางท่านด้วยครับ. จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : วันแม่แห่งชาติ 11:28:49

ความคิดเห็นที่ 96 #83,#88,#93,#94 มันมีหลายประเด็น (อ่านแล้วมึนดีเหมือนกัน :-) ขอลองแยกแยะดูนะครับ 1. สำหรับท่านผู้อ่านท่านอื่น ๆ ผมขอเสริมสิ่งที่คุณ packham อธิบายมานะครับ  ว่าคุณ packham อธิบายโดยใช้หลักการของคณิตศาสตร์ปัจจุบัน (ซึ่งนร. นักศึกษา ควรใช้ตามนี้)  โดยคุณ packham พูดถึง Field mathematics  ซึ่งเป็นส่วนสำคัญใน เรขาคณิต (algebra) ยุคปัจจุบัน อันมีตัวชูโรงหลัก ๆ ได้แก่ เรื่องของ  sets, operations, fields, groups, rings เป็นต้น  (ถ้าผมตกหล่นหรือพลาดไปตรงไหน ขอเชิญคุณ packham แก้ไขได้เลยนะครับ ไม่ต้องเกรงใจ :-)   เพราะว่าตอนนี้ ผมคงสอบทานได้แค่ เปิดหนังสือคร่าว ๆ หรือ google เอา ได้แค่นั้น) 2. 1/0 มีความหมายหรือไม่   ถ้าตอบบนกรอบคิด คณิตศาสตร์ที่ยอมรับกันในปัจจุบัน (Formalized mathematics)   ก็ต้องตอบว่า undefined และไม่มีความหมาย (meaningless) แต่อย่างใด   และผมคิดว่า ถ้าเห็นนักเรียนม.ปลายขึ้นไป เขียนว่า 1/0   น่าจะแทบร้อยทั้งร้อย ที่เขียนมันในเชิงว่ามันเป็น limit ของ 1/x เมื่อ x -> 0   (ซึ่งผลของมันก็คือ ค่าของ limit -> +infinity หรือ -infinity)   ซึ่งไม่ถูก ด้วยเหตุผลตามที่คุณ packham ชี้แจงไว้แล้วว่า 0 ไม่มีอินเวอร์สการคูณ   แต่ว่า ถ้าลองดูในประวัติคณิตศาสตร์ (History of mathematics)   จะพบว่า มีความพยายามหลายครั้ง ที่พยายามหาว่า 1/0 = ?   และส่วนใหญ่ก็หาไม่ได้ (เพราะถ้าสมมติให้มันเป็นอะไรสักอย่าง ก็จะพบว่ามันจะขัดแย้งกันเอง)   ซึ่งจะทำให้นำไปสู่ข้อสรุปที่ว่า 1/0 นั้น undefined   (ตรงนี้ ผมว่ามันต่างกันนิดเดียวกับการอธิบายว่า 1/0 นั้น undefined ก่อนลงมือหาคำตอบ)   แต่ถ้าเราลองเปลี่ยนกรอบคิดดู เช่นลดทอนระบบจำนวนลง ไม่ยอมรับว่ามีจำนวนลบ   เราอาจพบว่าได้ข้อสรุปที่เปลี่ยนไป   (ผมเข้าใจว่าความพยายามในอดีตส่วนใหญ่ จะเลือกกรอบคล้าย ๆ นี้ จึงสรุปว่า 1/0 = infinity   ทั้งนี้เราต้องไม่ลืมว่า Formalized mathematics ในปัจจุบันนั้น เราพึ่งมีกันซักราว ๆ สองร้อยปีนี้เอง    --ยังไม่ได้สอบทานเรื่องของเวลานะครับ แล้วก็ประวัติคณิตศาสตร์มันซับซ้อนกว่านั้น)   แต่ผมเคยบอกคุณ mint_la ไปว่า 1/0 นั้น มีบางสำนัก (หรือกรอบคิด) ที่ถือว่า = infinity ได้   นอกจากสำนักก่อนยุค rigour (formal) แล้ว   ผมคิดว่า ก็ยังมีบางกรอบคิดที่เป็นที่ยอมรับในปัจจุบัน ที่ยอมให้ 1/0 = infinity ได้ด้วย   อย่างน้อย ๆ ที่ผมพอจะทราบก็คือบน Reimann Sphere  เหตุผลง่าย ๆ ก็คือ บนนั้นทุก ๆ infinity มันจะไปรวมกันเป็นจุดจุดเดียว  (infinity ในที่นี้ จึงมีความหมายทั้งในแง่ของ +infinity และ -infinity ไปพร้อม ๆ กันครับ) 3. indeterminate form เป็น expression ใน context ของ limit ทั้งสิ้นหรือเปล่า   ผมเองก็ไม่แน่ใจเหมือนกัน เพราะพอใช้คำว่า indeterminate form มันจะไปอยู่ใน context ของ limit   แต่พอใช้แค่คำว่า indeterminate เฉย ๆ ผมกลับรู้สึกว่ามันเป็นแค่คำภาษาอังกฤษธรรมดา   ดังนั้น อาจจะมีที่ใช้ที่อื่นอยู่บ้างก็ได้   ที่สำคัญ ผมไม่แน่ใจว่าเมื่อ 300-400 ปีก่อนนี้ ภาษาอังกฤษมีบทบาทแค่ไหนแล้ว   และภาษาละตินยุคนั้น เขาใช้คำว่าอะไรกันแน่ แต่น่าจะมีคำที่รากศัพท์เกี่ยวข้องกัน ใช้กันอยู่บ้าง   อยากจะขอเสริมนิดนึงครับ ว่าที่คุณ packham คัดลอก (quote) จาก Wikipedia มานั้น   ข้อความประโยคแรกเต็ม ๆ เป็นอย่างนี้นะครับ      "In calculus and other branches of mathematical analysis, an indeterminate form      is an algebraic expression obtained in the context of limits. ..."   จะเห็นว่าผู้เขียนออกตัวไว้ก่อนแล้ว ว่าต้องการพูดถึง indeterminate form ภายใต้กรอบคิด   ของ calculus และสาขาอื่น ๆ ของ mathematical analysis เท่านั้น   ซึ่งผมคิดว่า เป็นการออกตัวที่ค่อนข้างปลอดภัยมากครับ :-) 4. infinity ก็เหมือนกันครับ infinity ไม่ใช่จำนวน เป็น concept ของ limit   ตรงนี้ ขออนุญาตเห็นต่างนะครับ เพราะคิดว่า concept ของคำว่า infinity นั้น เกิดมานานมากแล้ว   และผมค่อนข้างมันใจว่า แนวคิดเรื่อง infinity (อนันต์, อสงไขย, ฯลฯ) มีมาก่อน limit ครับ   เห็นด้วยประการหนึ่งว่า ในคณิตศาสตร์ปัจจุบัน เราไม่ถือว่า infinity เป็นจำนวน   แต่คิดว่า ในหลาย ๆ กรอบคิด มันน่าจะเป็นสิ่งที่อนิยาม (undefined terms) ครับ   คือทุกคนรู้ว่ามันคืออะไร   และบางกรอบคิด ก็จำเป็นต้องนิยามลงไป เพื่อหลีกเลี่ยงความคลุมเครือ 5. เรื่องของ infinitesimal นั้น    ผมคิดว่ามันน่าจะเป็นอนิยามนะครับ อีกประการคือ ผมคิดว่ามันถูกละเลยในคณิตศาสตร์ปัจจุบัน    ทั้ง ๆ ที่ความจริง กำเนิดของ calculus (โดย Newton และ Leibniz) นั้น ก็คือ Infinitesimal calculus    คิดว่าถ้าต้องการนิยามแบบที่เป็นปัจจุบันหน่อย คงต้องไปหาจากสาขา Non-standard analysis    ครับ ผมลองค้นเว็บดู ได้ชื่อ Abraham Robinson มา แต่คงไม่ค้นต่อเองประเด็นนี้ครับ เดี๋ยวจะลองอ่านความเห็นของท่านอื่น ๆ ต่อนะครับ. จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : วันแม่แห่งชาติ 12:32:59

ความคิดเห็นที่ 97 #94 คุณ packham ขอบคุณครับสำหรับคำตอบ 1. แสดงว่าผมจับความใน #83 ผิดเองครับ (ที่อ่านแล้วโยงย่อหน้า 8-9 ว่าเป็นเหตุสนับสนุน ย่อหน้า 10) ขออภัยด้วยครับ 2. ผมคงอธิบายให้กระจ่างไม่ได้ครับ แต่ผมบอกได้ว่ามีแนวคิดที่พัฒนา infinitesimal ต่อมาจาก ไลบ์นิซโดยใช้ standard part function (st) ใน non-standard calculus ผมคิดว่าหนังสือเล่มนี้อาจจะช่วยให้รายอะไรได้ Elementary Calculus: An Infinitesimal Approach http://www.math.wisc.edu/~keisler/calc.html แต่พอจับไอเดียการคำนวณอนุพันธ์ของ f(x) = x2 ซึ่งทั้งวิธีการใช้ infinitesimal กับลิมิตต่างยอมรับการจัดการเชิงพีชคณิตของ [(x + Dx)2 - x2]/Dx ในการณีของลิมิต เราก็หาลิมิตที่ Dx เข้าสู่ศูนย์ แต่ในกรณีของ infinitesimal ผมเข้าใจว่าเขาใช้ st แต่ก่อนหน้าที่จะใช้ st ตัวของไลบ์นิซเอง จะเรียกว่าอะไรดี หยั่งรู้ (intuition) กระมังครับ ว่า Dx คือ infinitesimal เมื่อจัดการกับ [(x + Dx)2 - x2]/Dx ตรง ๆ ได้ออกมาเป็น 2x + Dx จึงบอกว่าอนุพันธ์ของ f ที่ x คือ 2x (ตัด Dx ทิ้งเลย) เพราะว่า 2x + Dx แตกต่างจาก 2x ด้วย infinitesimal (ส่วนตัวผมมองว่าการเป็นการให้เหตุผลที่น่าทึ่งนะครับ - จากมุมมองของคนที่ไม่ใช่นักคณิตศาสตร์) จุดนี้ถูกบิชอบ Berkeley โจมตี Dx (infinitesimal) ของไลบ์นิซว่าเป็นผีของปริมาณที่ตาย (the ghosts of departed quantities) เพราะตอนแรกเพื่อให้ได้มาซึ่ง 2x + Dx ทำกับมันว่ามันมี (nonzero) แต่พอได้มาแล้วกลับเฉดหัวมันทิ้งไป (assumed zero) แต่ประเด็นผีนี้ตอนหลัง Abraham Robinson ก็แก้กลับโดยใช้ st ประเด็นคำถามนี้ของผมยังคงจุดยืนเดิมครับ คือไม่ได้คัดค้านว่าไม่ควรมอง 1/ฅ ด้วยปริมณฑลของลิมิต คำถามว่าจำเป็นหรือไม่ของผมจึงเป็นแค่ข้อสงสัยว่ามีเพียงวิธีมองแบบนี้วิธีเดียวเท่านั้นหรือ (ซึ่งโอเคคุณ packham ตอบแล้วว่าไม่จำเป็นนะครับ) สัญลักษณ์ 1/ฅ ถ้ามองแล้วชวนให้กังวลใจ ก็อาจเขียนแทนด้วย e แต่จุดมุ่งหมายของมันก็คือมีปริมาณ 1/x ที่น้อยกว่าค่าที่น้อยที่สุดในลำดับ 1/1, 1/2, 1/3, ... แก้ไขเมื่อ 12 ส.ค. 52 12:38:10 จากคุณ : ศล เขียนเมื่อ : วันแม่แห่งชาติ 12:35:41

ความคิดเห็นที่ 98 สวัสดีอีกครั้งครับคุณศล ตอบที่คุณศลถามมาใน #63 ครับว่าสบายดีครับ (อายุเพิ่มขึ้น<--แก่ลง อีกเล็กน้อย :-) และคิดถึงทุกคนเช่นกันครับ ขอนอกเรื่องสักนิดนะครับ ผมอ่านหลาย ๆ ความเห็นแล้ว จึงอยากจะเล่าว่าตอนที่ผมพิมพ์คำว่า meaningless ในหัวกระทู้นั้น มันเตือนผมว่ากรอบคิด หรือกรอบอ้างอิง (frame of reference) นั้นสำคัญทีเดียว เพราะถ้ากรอบคิดไม่ตรงกัน มันจะทำให้ออกความเห็นเรื่องเดียวกัน ไม่ตรงกันได้ง่าย ทั้ง ๆ ที่เป็นเรื่องเดียวกัน แต่มันเป็นคนละ context หลาย ๆ สิ่งที่แย้งกัน จึง meaningless ผมคิดว่าคนไทยสองสามปีให้หลังนี้ ก็ตกอยู่ในปัญหาเรื่อง "ความเห็นไม่ตรงกัน" โดยที่บางทียังไม่ทันคุยกันให้รู้เรื่องเลย ซึ่งน่าแปลกใจมาก เพราะความจริงการ "เอาใจเขามาใส่ใจเรา" เป็นคำสอนที่เราเคยได้ยินกันมาแต่อ้อนแต่ออก ถ้าปฏิบัติได้อย่างนั้น (คือสามารถปรับความคิดเรา โดยลองมองเรื่องเดิมด้วยมุมมองของคนอื่น) ผมคิดว่า ความขัดแย้งจำนวนมาก จะลดลงไปได้เอง และนำไปสู่ความเข้าใจ "ซึ่งกันและกัน" ได้ในที่สุดครับ และสิ่งที่เห็นขัดแย้งกัน (conflicts) จะลดรูปกลายเป็นการถกเถียงที่สร้างสรรค์ (healthy arguments) ครับ ผมเชื่ออย่างนั้น คือหลังจากถกกันเสร็จ อาจจะไม่มีใครเปลี่ยนจุดยืนก็ได้ แต่ว่าแต่ละคน ต่างก็จะเข้าใจทั้งตัวเอง และผู้อื่น ได้ลึกซึ้งขึ้น ซึ่งเป็นเรื่องที่ดีมาก ๆ คุณศลออกตัวว่า นอกกระแส แต่ผมกลับคิดว่า คณิตศาสตร์นั้น มันหมายความรวมคณิตศาสตร์ทุกแขนง ทั้งที่เป็น Formalized mathematics และสาขาอื่น ๆ ตลอดจนคณิตศาสตร์ในอดีต และในอนาคตด้วย แน่นอนว่า ในยุคของเรา ต้องถือว่า Formalized mathematics เปรียบเหมือนเสาหลัก แต่ใครจะรู้ว่า ในอนาคต concepts พื้นฐานต่าง ๆ จะต้องถูกชำระกันอีกกี่ครั้ง ในรอบร้อยปีหลังนี้ เรามีคณิตศาสตร์ที่สวนความคิดเดิม ๆ มากมาย ไม่ว่าจะเป็น hyperreal number, fuzzy logic, fractal geometry, fractional summation, chaos theory, ฯลฯ ดังนั้น ผมคิดว่าไม่มีใครสวนกระแส เพราะกระแสนั้น ไม่ใช่สิ่งที่จีรังยั่งยืนครับ (ที่จริง ผมคิดว่า ในอุดมคติของแวดวงวิทยาศาสตร์นั้น ไม่ควรมีการตามกระแสด้วยซ้ำไป) ------------------------------------------------------- เพิ่มเติม: คุณศลได้ชื่อ Abraham Robinson มาเหมือนกันเลย แถมยังได้รายละเอียดเพิ่มเติมด้วย อีกพอสมควร ถ้ามีเวลา ก็อยากจะอ่านให้ละเอียดเหมือนกัน ขอบคุณครับ แก้ไขเมื่อ 12 ส.ค. 52 15:45:35 จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : วันแม่แห่งชาติ 13:06:20

ความคิดเห็นที่ 99 #55,#90,#91 สำหรับประเด็นที่แย้งมาว่า ต้องแสดงให้เห็นก่อนว่า A(0/0) = A จึงจะบอกได้ว่า 0/0 can be many things ได้นั้น ขออนุญาตไม่แสดงเองนะครับ เพราะคิดว่าคุณเซียนแห่ง math น่าจะทราบดีอยู่แล้ว สำหรับท่านอื่น ๆ ที่อยากทราบว่าจะแสดงอย่างไร ลองอ่านที่นี่ดูครับ http://www.math.utah.edu/~pa/math/0by0.html ซึ่งจะเป็นการใช้ความคิดแบบ informal proof ซึ่งจะได้ผลเป็น contradiction แล้วสุดท้าย จะสรุปว่า เพราะว่ามัน can be many things ดังนั้น มันจึงเป็นสิ่งที่ undefined ครับ ส่วนเรื่องที่คุณ mint_la ถามมาว่า ที่ไหนที่เขายอมให้ 1/0 = infinity คำตอบนั้น ผมบอกไว้ใน #96 ข้อ 2 แล้วครับ แนวคิดสำคัญที่ทำให้มันเป็นไปได้ คือเรื่อง point at infinity ผมลองเปิดหนังสือดู พบว่าคนแรกที่เอ่ยถึงแนวคิดเรื่อง point at infinity นี้ คือ Kepler ครับ และได้ถูกต่อยอดมาเป็นระยะ ๆ จนกระทั่งสุดท้าย พบเรื่องนี้ภายใต้ชื่อของ Reinmann ครับ. จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : วันแม่แห่งชาติ 13:17:54

ความคิดเห็นที่ 100 เป็นปลื้ม ^^" ขอบคุณคุณลุงแว่นใจดีค่ะ ยังคงความเป็นนักวิเคราะห์ ที่ยอดเยี่ยมได้เสมอมา "มองออก" ในทุกๆความหมาย เปี่ยมด้วยควมรู้ เป็นผู้ฟังที่ดี เป็นครูที่ดี แล้วนำเสนอได้อย่างยอดเยี่ยม สมบูรณ์แบบ จากคุณ : หลานแว่น (mint_la) เขียนเมื่อ : วันแม่แห่งชาติ 13:44:14

ความคิดเห็นที่ 101 สวัสดีครับ ขอร่วมพัฒนากระทู้ ดีมากๆ อย่างนี้ซักคนนะครับ ผมได้ความรู้และแนวคิดมากมายจากคำตอบของแต่ละท่าน แต่ส่วนตัวผมอยากให้ยืนยันเป้าหมายในการหาข้อสรุปที่แข็งกว่านี้ เพราะ การคุยแนวทางนี้ เรายังไม่เข้าใกล้คำตอบมากพอ มันจะกลายเป็นคนนั้นก็ถูก ในกรอบนั้น คนนี้ก็ถูกในกรอบนี้ไป จึงควร normalise มันเท่าที่จะทำได้ก่อน เราก็จะได้ขอสรุปที่ คล้ายๆข้อสรุปในอุดมคติ หลังจากนั้น ค่อย แลกเปลี่ยนความเห็น หรือขยายกรอบพิจรณาออกไปในฝั่งของ Application เพราะอย่างที่ทราบกัน แต่ละปัญหา ที่มี Infinity ไปเกี่ยวข้องนั้นมีกรอบพิจราณา และความยากง่ายไม่เท่ากัน และที่สำคัญส่วนใหญ่แล้ว การตีความ จำนวนใดๆ ให้เป็น Infinity นั้น(โดยเฉพาะ ฟิสิกส์ ) ไม่ใช่การตีความที่สมบูลย์ มีคำตอบได้หลากหลาย ความถูกผิดไม่เท่ากัน คุณลุงแว่นใจดี นั้นได้ normalise องค์ประกอบต่างๆไว้อย่างละเอียดที่สุดแล้ว แตุ่ถ้าจะนำ้มาซึงคำตอบที่ใกล้เคียงมากขึ้น ผมขอเสนอให้ normalise  กรอบในการพิจารณาด้วย ซึ่งผมเห็นไปในแนวทางเดียวกับ คุณลุงแว่นใจดีดังที่ ผมจะขอเริ่มต้นด้วย การเสนอสัจพจน์เพิ่มเติมดังนี้ 1 คำว่าคณิตศาสตร์ในกระทู้นี้  ผมขอเสนอให้หมายถึงคณิตศาสตร์บริสุทธ ให้สมกับ บทบาทหลักๆของมัน 2 0 หมายถึง 0 จริงๆ ไม่ใช่เข้าใกล้ 0 หรือมันควรต้องเป็น 0   ถ้ามีใครอยากเพิ่มเติมเพื่อประโยชในการพิจรณาจะดีมากเลยครับ ส่วนตัวผมขอเริ่มต้นที่ 2 ข้อนี้เพื่อจะได้ร่วมตอบคำถาม ก่อนนะครับ 1/0 = ? ถ้าเรามองความหมายมันว่า 1 ส่วนใน 0 ส่วน คำตอบของผม นั้น ยืนยันตามที่เราทราบกันครับว่า 1/0 = ไม่นิยาม คือไม่ใช่คำตอบที่ ทีมีคำตอบ และคณิตศาสตร์ไม่ได้ถูกออกแบบมาให้ตอบคำถามนี้ หมายความง่ายๆว่า ใช้คณิตศาสตร์เปล่าๆมาตอบไม่ได้ ถ้าเรามองความหมายมันว่า 0 คูณอะไรได้ 1 คำตอบคือ ไม่มีบนแกนจำนวนจริง ( ถ้าในธรรมชาติ เราพบเงื่อนไขนี้ จริง ก็จำเป็นต้องพัฒนาคณิตศาสร์แบบขยายขึ้นมาเพื่ออธิบายมัน คล้ายๆ แกนของจำนวนเชิงซ้อน ซึ่งแน่นอนว่าในฐานะนักวิทยาศาสตร์เรายังไม่เชื่อว่าจะมีอะไรที่เกิดขึ้นมาจากการไม่มีได้ ) คำตอบที่ถูกต้องบนกรอบพิจรณานี้จึงควรจะเป็น (Undefined+ไม่มีคำตอบ)/2 = Undefined ซึ่งแน่นอนว่า คณิตร์ศาตร์ไม่มีความหมายในตัวเอง การตอบคำถามนี้ จึงไม่มีประโยชใด้ๆ จนกว่าเราจะใส่ Application ให้มัน ดังคำตอบที่หลากหลายอันเป็นความรู้ ข้างบน จากคุณ : +5 Coulomb เขียนเมื่อ : วันแม่แห่งชาติ 14:32:42

ความคิดเห็นที่ 102 #58 คุณ nonlocality ถ้าถามผม ผมกลับคิดว่าคุณ nonlocality ไม่ได้ผิดตรงไหน แล้วก็ไม่ได้เบี่ยงประเด็นกระทู้อะไร ผมว่าการพยายามมองหาว่า concept ต่าง ๆ ที่เรามีในคณิตศาสตร์นั้น ใช้ในชีวิตได้อย่างไรบ้าง เป็นสิ่งที่ควรสนับสนุนครับ ผมจำได้ว่าก่อนจะมี Discovery, National Geography, History Channel, ฯลฯ มีรายการที่นักวิทยาศาสตร์ ออกมาคุยเรื่องวิทยาศาสตร์ที่ประยุกต์กับชีวิตประจำวันได้ (ที่ผมจำได้ ก็คือ Carl Sagan) ซึ่งทำให้เกิดคำใหม่ว่า Popular Science ขึ้นมา ถึงอาจจะมีนักวิทยาศาสตร์บางคน ดูแคลนเอาว่ามันเป็น Pseudoscience แต่ผมเห็นว่า มันมีประโยชน์ และกระตุ้นให้คนรุ่นต่อมา สนใจวิทยาศาสตร์มากขึ้นกว่าเดิมมากครับ #62 คุณ panote_saechiew fractal นี่มีความยาวเป็นอนันต์รึเปล่า ผมก็ไม่ทราบเหมือนกันครับ ไม่สันทัดกรณีนี้เสียด้วย แต่จำได้ว่า คำถามเชิง fractal แบบพื้น ๆ ที่พอจำได้ ก็เช่น เราไม่สามารถวัดความยาวของประเทศได้ (เพราะทุกการวัด ก็จะเป็นเพียงการประมาณ ที่จริงยังมี fractal ในระดับที่เล็กกว่าไม้วัดของเราเสมอ) #65 คุณ P.Virie โยงเรื่องของอนันต์ เข้ากับความต่อเนื่อง เข้าท่าดีครับ ถ้าจำไม่ผิด ตอนที่ Newton เริ่มคิดเรื่อง limit, caclulus ก็คิดในแง่ของความต่อเนื่อง เช่นกันครับ แต่ที่สงสัย คือ ถ้าความยาวจาก 0 ถึง 1 ไม่เท่ากับ 1 ถึง 2 นอกจากบนสเกลที่ไม่ปกติ (เช่น logarithm) แล้ว มันมีที่ไหนอีกหรือเปล่าครับ (อ่านแล้วชวนให้คิดว่าคุณ P.Virie หมายถึงบน model อะไรสักอย่าง) #71 คุณ unholy 00 เป็นหนึ่งใน indeterminate form ครับ ดังนั้นโดยทั่วไปแล้ว คงต้องบอกว่า indeterminate แต่ว่าใน Concrete mathematics (น่าจะเป็น Discrete math.), Donald Knuth แย้งว่าควรเป็น 1 โดยให้เหตุผลว่าอย่างนี้ครับ   Some textbooks leave the quantity 00 undefined, because the functions 0x and x0 have   different limiting values when x decreases to 0. But this is a mistake. We must define x0 =1 for all x,   if the binomial theorem is to be valid when x=0, y=0, and/or x=-y . The theorem is too important   to be arbitrarily restricted! By contrast, the function 0x is quite unimportant. #72 คุณ ONaja สวัสดีครับ สบายดีนะครับ ตอนนี้จำได้แล้วครับ (ตอนแรกก็ลืมเหมือนกัน แหะ ๆ) #79 คุณ aLITTLEspaceAround7day อ่า... เอ่อ... เอางี้ครับ อยากให้ลองคิดดูก่อนครับ ว่า 1/0 ของคุณ aLITTLEspaceAround7day หมายถึงอะไรกันแน่ ก่อนจะเอามาบวกกันน่ะครับ (- -" ปาดเหงื่อเล็กน้อย) ขอบคุณทุกท่านที่เข้ามาแสดงความเห็นด้วยครับ. จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : วันแม่แห่งชาติ 15:14:40

ความคิดเห็นที่ 103 #101 คุณ +5 Coulomb ยินดีครับ ที่แวะเวียนเข้ามา ตอนแรกผมอ่านคคห.ของคุณ +5 Coulomb ก็งง ๆ อยู่เหมือนกัน (คงไม่ค่อยคุ้นสำนวนน่ะครับ) พอจับความได้แล้ว ก็คิดว่าเห็นด้วยเป็นส่วนใหญ่ครับ แต่ก็มีบางประเด็น ที่อยากจะขอออกความเห็นเพิ่มเติม สักเล็กน้อยครับ - โดยเนื้อแท้แล้ว ผมไม่ได้อยากให้กลายเป็น "คนนั้นก็ถูกในกรอบนั้น คนนี้ก็ถูกในกรอบนี้" ครับ   แต่อยากเห็นทุกคน เข้าใจว่า ในแต่ละกรอบนั้น ที่ถูกแล้ว เป็นอย่างไร มากกว่าครับ - อันนี้ไม่ซีเรียส (แต่ทำผมมึนเหมือนกัน)   คือผมว่า ถ้าเลี่ยงคำว่า สัจพจน์ มาใช้คำว่า หลักเกณฑ์ หรือกติกา น่าจะดีกว่าครับ   คำว่า สัจพจน์ ค่อนข้างแรงไปนิด และมีความหมายที่ชัดเจนไปแล้ว ถ้าเลี่ยงได้ ก็จะดีกว่าครับ - ทั้ง 2 หลักเกณฑ์ ที่คุณ +5 Coulomb เสนอมา   ผมเข้าใจว่า ทุกคนก็ทราบและใช้ตามนั้นอยู่แล้ว แต่พอเห็นที่คุณ +5 Coulomb เขียนมา   ก็เลยทำให้นึกขึ้นได้ว่า ความจริง อาจมีบางคน เห็นเป็นอย่างอื่นก็ได้ ดีเหมือนกันครับ   คือสำหรับผม โดยทั่วไป ถ้าไม่ระบุเป็นอย่างอื่น ก็ควรใช้คำนั้นในความหมายที่คนทั่วไปเข้าใจครับ   ดังนั้น 0 ก็ควรเป็น 0 ไม่ใช่อะไรที่เข้าใกล้ 0   (ยกเว้นในกระดาษทด หรือสมุดโน้ต ที่เขียนไว้อ่านคนเดียว จะย่อยังไงก็คงไม่มีใครว่าครับ) - (Undefined+ไม่มีคำตอบ)/2 = Undefined   เป็นบรรทัดที่งงที่สุดครับ อันนี้มาจากที่เคยคุยกันไว้ ก่อนที่ผมจะเข้ามาหรือเปล่าครับ จากคุณ : ลุงแว่นใจดี เขียนเมื่อ : วันแม่แห่งชาติ 15:30:51

ความคิดเห็นที่ 104 ... เข้ามาดู จากคุณ : loverpool เขียนเมื่อ : วันแม่แห่งชาติ 18:28:55

ความคิดเห็นที่ 105 สวัสดีครับ ดีใจที่ได้ร่วมพูดคุยครับ คุณลุงแว่นใจดี ขอชี้แจงตามนี้นะครับ - โดยเนื้อแท้แล้ว ผมไม่ได้อยากให้กลายเป็น "คนนั้นก็ถูกในกรอบนั้น คนนี้ก็ถูกในกรอบนี้" ครับ  แต่อยากเห็นทุกคน เข้าใจว่า ในแต่ละกรอบนั้น ที่ถูกแล้ว เป็นอย่างไร มากกว่าครับ /// จริงๆแล้ว ผมไม่ได้หมายความรุนแรงขนาดนั้นครับผม  หวังว่าคงเข้าใจเจตนานะครับ - อันนี้ไม่ซีเรียส (แต่ทำผมมึนเหมือนกัน)  คือผมว่า ถ้าเลี่ยงคำว่า สัจพจน์ มาใช้คำว่า หลักเกณฑ์ หรือกติกา น่าจะดีกว่าครับ  คำว่า สัจพจน์ ค่อนข้างแรงไปนิด และมีความหมายที่ชัดเจนไปแล้ว ถ้าเลี่ยงได้ ก็จะดีกว่าครับ /// อันนี้ต้องขอโทษด้วยครับ ผมพยายามตอบโดยใช้องค์ประกอบที่แจงไว้ข้างต้นกระทู้ ให้มากที่สุดนะครับ แต่ก็พึ่งทราบเหมือนกันว่า มีวิธีใช้ซีเรียสขนาดนี้ ต้องขอบคุณครับ จะระวังครับ จริงๆแล้วผมไม่ใช่คนที่มีสิทรกำหนดกติกาหนะครับ เลยต้องเสนอเป็น สัจพจน์ สำหรับกระทู้นี้ ในหัวข้อที่ เข้าใจเอาเองว่า ทุกคนเห็นด้วยอยู่แล้ว ไม่ต้องพิสูจ ประมาณว่าถ้าใครไม่ยอมรับตามนี้ ก็ไม่แปลกถ้าจะไม่เห็นด้วยกับคำตอบผม คือผมคิดเอาเองว่ามันรัดกุมนะครับ - ทั้ง 2 หลักเกณฑ์ ที่คุณ +5 Coulomb เสนอมา  ผมเข้าใจว่า ทุกคนก็ทราบและใช้ตามนั้นอยู่แล้ว แต่พอเห็นที่คุณ +5 Coulomb เขียนมา  ก็เลยทำให้นึกขึ้นได้ว่า ความจริง อาจมีบางคน เห็นเป็นอย่างอื่นก็ได้ ดีเหมือนกันครับ /// ขออนุญาต อธิบายครับ ผมไม่ได้ตั้งใจว่า ให้คนที่ไม่ทราบได้ทราบ หรือคิดว่าทุกคนไม่ทราบจึงเขียน แต่ทำเพื่อการ กำหนดกรอบสนทนาที่เล็กที่สุดก่อน ประมาณว่าขอความเห็นด้วยว่า  " ต่อไปนี้เรามาคุยกันภาบใต้กรอบนี้นะ เอาเฉพาะที่เพียวๆ ก่อน แล้วพอเห็นตรงกันแล้ว ค่อยขยายความต่อ"  <<<< ประมาณนี้หนะครับ  คือสำหรับผม โดยทั่วไป ถ้าไม่ระบุเป็นอย่างอื่น ก็ควรใช้คำนั้นในความหมายที่คนทั่วไปเข้าใจครับ  ดังนั้น 0 ก็ควรเป็น 0 ไม่ใช่อะไรที่เข้าใกล้ 0  (ยกเว้นในกระดาษทด หรือสมุดโน้ต ที่เขียนไว้อ่านคนเดียว จะย่อยังไงก็คงไม่มีใครว่าครับ) //เห็นด้วยครับ ข้อนี้ผมเขียนเพื่อ ตัด คำถามบางคำถามที่พอจะเดาได้ และ ไม่มีประโยชน์ที่จะตอบที่ สเตจนี้ออก เพราะอยาก นอมอลไร้ส์ ก่อนนะครับ - (Undefined+ไม่มีคำตอบ)/2 = Undefined  เป็นบรรทัดที่งงที่สุดครับ อันนี้มาจากที่เคยคุยกันไว้ ก่อนที่ผมจะเข้ามาหรือเปล่าครับ // ไม่ใช่ครับเป็นการอธิบายแบบของผมเอง  ทำนองว่า (หิน+เศษหิน)/2 ยังไงมันก็เป็นหิน (เอาหิน มากองรวม กับเศษหิน แล้วเอาออกคริงนึง ก็จะได้กองหิน )ผมว่าเข้าท่าออก ^^   จริงๆผมว่าการเอา Math มาใช้มันก็ต้องอย่างนี้แหละครับ มันส์ ดี ประมาณนี้ครับ Undefined+Undefined = 2 Undefined = Undefined << ในกรณีนี้ สองเท่าของไม่นิยาม ก็ต้องเป็น ไม่นิยามสิ จริงมั้ยครับ ต้องขอโทษสำหรับภาษาของผมนะครับ เพราะผมพิมไม่เก่งนะครับ นึกไม่ออกว่าตัวไหนมันอยู่ตรงไหน ก็เลยมั่วๆไป ทำจนเป็นนิสัยแล้วหละครับ แก้ไขเมื่อ 12 ส.ค. 52 19:36:39 แก้ไขเมื่อ 12 ส.ค. 52 19:33:20 แก้ไขเมื่อ 12 ส.ค. 52 19:27:22 จากคุณ : +5 Coulomb เขียนเมื่อ : วันแม่แห่งชาติ 19:22:43

ความคิดเห็นที่ 106 ผมอ่านหนังสือ การปฏิวัติสัญศาสตร์ของโซซูร์ เขียนโดยธีรยุทธ บุญมี มีบางตอนเขียนว่า รุสโซว่าประโยคแรกที่คนเอ่ยเป็นคำอุทาน ไม่ใช่ตรรกะ สิ่งที่ครอบงำทัศนคติคืออารมณ์ ความรู้สึก ไม่ใช่เหตุผล โซซูร์ว่า ภาษากับความคิดไม่สัมพันธ์ที่จะคาดเดา หรืออนุมานจากสิ่งหนึ่งไปอีกสิ่ง Sapir ว่า ภาษาต่างกันกำหนดรูปแบบความคิดแต่ละกลุ่มให้ต่างกัน ทำนองเดียวกัน คณิตศาสตร์มีหลายสาขา อาจนับว่าเป็นหลายภาษาเช่นกัน ดังนั้นเมื่อพูดถึงเรื่องคณิตศาสตร์ อาจต้องระบุลงไปว่าคณิตศาสตร์สาขาใด เช่น 1/0 จะพูดในเรื่องจำนวนจริงหรือ Calculus      1+1=2 ในเรื่องจำนวนจริง หรือ 1+1=1 ใน Boolean Algebra OR Operations (+)      1+1 = 1      A+A' = 1 http://www.play-hookey.com/digital/boolean_algebra.html ความคิดเห็นที่ 96   5. infinitesimal น่าจะอนิยาม calculus (โดย Newton และ Leibniz) นั้น ก็คือ Infinitesimal calculus คิดว่า infinitesimal ใน Calculus คือสิ่งที่จิ๊วจิ๋ว เล็กจนไม่อาจเล็กกว่านี้ "infinitesimal" in the vernacular means "extremely small" http://en.wikipedia.org/wiki/Infinitesimal ทำให้คิดว่าอาจเป็นความหมายคล้ายควอนตัม- Quantum เช่น โฟตอนอาจถือว่าเป็นอนุภาคเล็กที่สุดของแสง หรือโฟตอนคือ infinitesimal ของแสง จากคุณ : ชื่อนี้ได้มั้ยฮะ เขียนเมื่อ : วันแม่แห่งชาติ 20:57:44