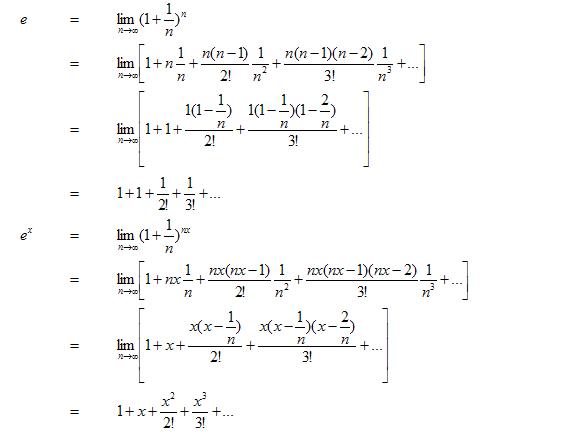ความคิดเห็นที่ 1 เอ่อ ลืมไป ถ้าเก่าแล้วก็ขออภัย แบบว่า... เพิ่งรู้อ่ะ... คนอื่นอาจรู้อยู่แล้วแฮะ... >_< จากคุณ : Little Humming Bug เขียนเมื่อ : 16 ส.ค. 52 09:19:41

ความคิดเห็นที่ 2 การหาอนุพันธ์นั้นมีนิยามอยู่แล้วครับ คุณอาจเพียงข้ามหรือจำไม่ได้ในส่วนที่เป็นการนิยามก่อนจะมาเป็นสูตรในการหาอนุพันธ์หรือการอินทิเกรต ลองย้อนกลับไปอ่านส่วนต้นก่อนที่จะมาเป็นสูตรในการหาอนุพันธ์ก็จะเข้าใจเองครับ จากคุณ : Koongie เขียนเมื่อ : 16 ส.ค. 52 09:28:04

ความคิดเห็นที่ 3 ไม่ใช่นิยามครับ มันมีที่มาของนิยามครับ ตอนที่เราเรียนกันสมัย cal1 cal2 นั่นเราเรียนตามนิยาม แต่เบื้องหลังนิยามมันมีคำอธิบายทุกเรื่องครับ... และคำอธิบายมักจะอยู่นอกตำราเรียน อย่างที่ผมยกตัวอย่างสมัยประถม ในตำราก็จะมีแต่สูตรพื้นที่วงกลม พื้นที่ผิวทรงกลม บลาๆๆ ถ้าอาจารย์ผู้สอนสอนตามตำรา เด็กก็ได้แต่ท่องจำครับ สิ่งที่ผมถามนี่มันนอกตำราอ่ะครับ นิยามที่ว่าผมก็จำได้ มักจะเขียนเป็นอรัมภบทสั้นๆ ก่อน ตามด้วยสมการน้อยๆ ล้อมกรอบสี่เหลี่ยม นิยาม d(e^x)/dx = e^x มันมีที่มาครับ อธิบายได้ด้วย จากคุณ : Little Humming Bug เขียนเมื่อ : 16 ส.ค. 52 10:11:08

ความคิดเห็นที่ 4 มันมีที่มา ต้องไปเปิดหนังสือ cal 1 น่ะมีแน่ เกี่ยวกับเรื่อง limit น่ะ เขาหาได้จากนิยามของอนุพันธ์ไงคะ โดยใช้ลิมิต คือf'(x) = lim fx - f(x+deltaxx) / delta x   x ใกล้ 0 จากคุณ : นู๋นัน เขียนเมื่อ : 16 ส.ค. 52 10:21:34

ความคิดเห็นที่ 5 กำลังเรียนอยู่เลยครับ งงๆ จากคุณ : Put'me เขียนเมื่อ : 16 ส.ค. 52 10:57:30

ความคิดเห็นที่ 6 คคห.4 ผมลองแล้วครับ ลองตรงๆ ทำยังไงก็ไม่ออกครับ lim [(e^(x +dx) - e^x)/dx] ลองตรงๆ ดูผมคิดไม่ออกครับ แต่จะว่าไป เทลเลอร์ดูก็น่าจะได้ แต่ก็จะเกิดคำถามต่อไปอีก แล้วเทลเลอร์มาได้ยังไง... แก้ไขคำผิด ตามคำแนะนำ คคห.14 ครับ ขอบคุณมาก (แล้วออยเลอร์มันเป็นใครฟระ? >_< ) แก้ไขเมื่อ 16 ส.ค. 52 20:01:00 จากคุณ : Little Humming Bug เขียนเมื่อ : 16 ส.ค. 52 11:15:02

ความคิดเห็นที่ 7 ลองคิดจาก series อีกทางดูครับ จาก http://en.wikipedia.org/wiki/Exponential_function e^x = e^x = 1 + x + x^2/2! + x^3/3! + ... d(e^x)/dx = 0 + 1 + 2x/2! + 3x^2/3! + ...           =  1 + x + x^2/2! + ...           = e^x อันนี้ต่อยอดจาก series ครับ ผมคิดว่ามันน่าจะต่อยอดจากนิยามอย่างอื่นได้อีก เพราะทุกอย่างคือสิ่งเดียวกัน หุหุ แก้ไขเมื่อ 16 ส.ค. 52 11:20:04 จากคุณ : 5Z เขียนเมื่อ : 16 ส.ค. 52 11:18:50

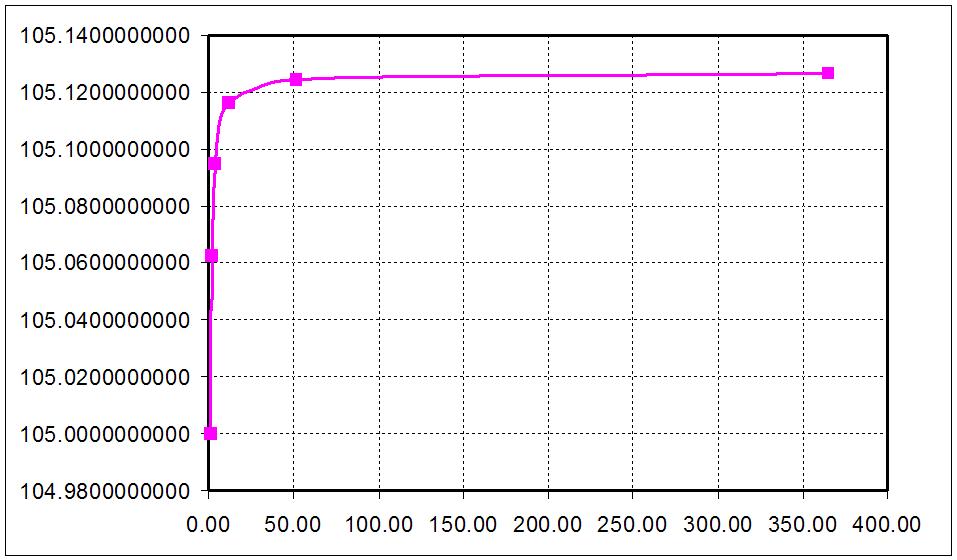
ความคิดเห็นที่ 8 ใช่เลยครับ ตาม คคห.7 มันคือสิ่งนั้นแหละครับ แต่ที่ถามต่อไปอีก นั่นแหละครับ ว่า e^x = 1 + x + x^2/2! + x^3/3! + ... มาได้ยังไง... ผมชอบที่มาของมันมากเลยครับ มันใกล้ตัวเหมือนกัน ตัว e เนี่ย e = lim (1+1/n)^n แม้กระทั่งนิยามนี้ ก็มีที่มาครับ เพิ่มเติม: อ่านตาม link ที่ คคห.7 แปะมาให้ มันตอบคำถามได้หมดเลยอ่ะครับ แหะแหะแหะ... ที่มาของ e ก็มาจาก Continuous compounding ซึ่งทีว่าใกล้ตัว ก็เพราะว่า มันเอามาใช้คิดพวกดอกเบี้ยเงินฝากอะไรพวกนั้นด้วย อย่างที่ว่า หากถอนเงินออกตอนไม่ครบปีแล้ว ธนาคารเขาจะให้ดอกเบี้ยเราเท่าไหร่กันแน่ คิดกันยังไง พวกเราเคยสงสัยกันบ้างหรือเปล่า? ผมก็ไม่รู้หรอกครับแต่เดาว่าน่าจะใช้ Continuous compounding เนี่ยแหละมาคิดให้พวกเรา หรือว่า เราฝากเงินไว้กับบัญชีหนึ่งก็ได้รับดอกเบี้ยปีละหนมาเรื่อยๆ วันดีคืนดีธนาคารโทรมาโฆษณาบัญชีเงินฝากแบบใหม่ คิดดอกเบี้ยปีละสองหน หรือปีละสี่หน หรือเดือนละหน หรือวันละครั้งเลยก็ยังได้ โดยอัตราดอกเบี้ยเป็นแบบ r/2, r/4, r/12, r/365 ตามลำดับ โดย r คืออัตราดอกเบี้ยรายปี อย่างเงี้ย เป็นเรา เราจะยอมถอนเงินจากบัญชีเดิมออกไปใส่ับัญชีใหม่ที่ธนาคารเสนอให้หรือเปล่า????? แก้ไขเมื่อ 16 ส.ค. 52 11:48:45 จากคุณ : Little Humming Bug เขียนเมื่อ : 16 ส.ค. 52 11:41:46

ความคิดเห็นที่ 9 เอาตาม คคห.7 เลยละกันนะครับ ขอบคุณครับ จากคุณ : Little Humming Bug เขียนเมื่อ : 16 ส.ค. 52 12:03:10

ความคิดเห็นที่ 10   "The most powerful force in the universe is compound interest" -Albert Einstein- ที่จริงมันน่าจะลึกซึ้งกว่านั้นนะ คล้ายๆหนังสือเรื่อง a history of pi (ยังหาเวลาอ่านไม่ได้เลย) แก้ไขเมื่อ 16 ส.ค. 52 12:07:47 จากคุณ : GlasNost เขียนเมื่อ : 16 ส.ค. 52 12:07:01

ความคิดเห็นที่ 11 ส่วนที่มาของ e ก็คือ เริ่มจากตัวอย่างเรื่องอัตราดอกเบี้ย กรณีแรกให้เป็นเงินฝากที่มีการจ่ายดอกเบี้ยรายปี ปีละหน เงินต้น P ฝาก 1 ปีปลายปีก็จะได้เงิน A1 = P(1+r/100)^t1 ตรงนี้เนี่ย r เป็นอัตราดอกเบี้ยรายปี หน่วยเป็น % นะครับเลยหาร 100 ส่วน t1 เป็นระยะเวลา หน่วยปี แต่หากธนาคารมีโปรฯ ใหม่ จ่ายดอกเบี้ยรายไตรมาส คือปีละสี่หน ฝากครบสามเดือนก็จะได้ A2a = P(1+r/4/100)^t2 โดย r ยังคงเป็นอัตราดอกเบี้ยรายปี แต่คราวนี้ต้องหาร 4 แล้ว t2 ก็เป็นระยะเวลาหน่วย 3 เดือน เงินก้อนแรก A2a นี่จะถือเป็นเงินต้นของไตรมาสถัดไป ฝากต่อก็จะคูณเทอมในวงเล็บต่อไปอีก เมื่อฝากครบปีเหมือนกับกรณีแรก ก็จะได้เงิน A2 = P x [(1+r/4/100)^t2]x[(1+r/4/100)^t2]x[(1+r/4/100)^t2]x[(1+r/4/100)^t2] = P(1+r/4/100)^4t2 ถ้ามีโปร 12 เดือน ก็จะได้ A3 = P(1+r/12/100)^12t3, t3 เป็นหน่วยเดือนละ โปร 365 วันก็จะได้ A4 = P(1+r/365/100)^365t4, t4 เป็นหน่วยวันเลยทีนี้... ถ้าแบ่งช่วงเวลาด้วยตัว s ก็จะได้ A = P(1+r/s/100)^s*t ผมลองคำนวณดูความสัมพันธ์ระหว่าง A กับ s ดู ดูว่า s ยิ่งมากจะยิ่งเป็นยังไง เราจะได้เงินเพิ่มกว่าการฝากรายปีหรือเปล่า ได้ผลอย่างนี้ครับ เงินต้น 100 บาทนะครับ r = 5% ดูเงินกันตอนปลายปีเลย s A 1 105.0000000000 ==> รายปี 2 105.0625000000 ==> รายครึ่งปี 4 105.0945336914 ==> รายไตรมาส 12 105.1161897882 ==> รายเดือน 52 105.1245841927 ==> รายสัปดาห์ 365 105.1267496467 ==> รายวัน แก้ไขเมื่อ 16 ส.ค. 52 12:54:19 จากคุณ : Little Humming Bug เขียนเมื่อ : 16 ส.ค. 52 12:17:34

ความคิดเห็นที่ 12 ผลก็คือ ยิ่งซอยย่อยระยะเวลาการจ่ายเงินให้กับเราถี่มากเท่าไหร่ เราก็จะยิ่งได้เงินมากขึ้น แต่มันจะมีจุด limit อยู่ครับ เหมือนในรูปเนี้ย จากคุณ : Little Humming Bug เขียนเมื่อ : 16 ส.ค. 52 12:21:09

ความคิดเห็นที่ 13 และนั่นก็คือ เหมือนกับ คคห.10 "The most powerful force in the universe is compound interest" เพราะว่า ไม่มีอะไรที่จะเกิน limit ของสมกานั้นได้ครับ ไม่ว่าค่า s จะมากแค่ไหน aka ไม่ว่าจะซอยย่อยเวลาลงไปให้ถี่มากแค่ไหนก็ตาม อิอิอิ... A = P(1+r/s/100)^st แล้วให้ r/s/100 = 1/n ก็จะได้ s = nr/100 ชิมิ... A = P(1+1/n)^(nrt/100) = P[(1+1/n)^n]^(rt/100) เขาก็เลยนิยามให้ e = lim(1+1/n)^n เมื่อ n ==> inf ก็คือ กรณีที่เรามองอัตราการเติบโตแบบต่อเนื่องไปเลย คือ ช่วงเวลาซอยย่อยถี่มากๆๆๆๆๆๆ ซึ่งก็คือค่าสูงสุดที่เราจะได้จากอัตราการเติบโตแบบคล้ายๆ กับเรื่องดอกเบี้ยเนี่ยครับ พูดง่ายๆ ก็คือเราไม่มีทางได้เงินเกินจากสมการค่า e ได้หรอกครับไม่ว่าธนาคารเขาจะเสนอโปรฯ ให้เราคิดดอกเบี้ยแบบถี่ยิบแค่ไหนก็ตาม... ได้เท่านี้แหละ A = Pe^(rt/100) ที่ Einstein พูดว่างั้น ก็เพราว่าค่า e มันเป็นธรรมชาติของหลายๆ อย่างตั้งแต่เรื่องใกล้ตัวอย่าง อัตราดอกเบี้ย ไปยังเรื่อง อัตราการเติบโตของประชากร ทั้งคน เื้ชื้อโรค ฯลฯ แล้วฟิสิกส์อีกสารพัดสารเพนั้น มันก็มักจะมาจาก สมการรูปแบบ d(f(x))/dx = k*f(x) แม้กระทั่งสมการนั่งเทียนอย่างชโรดิงเจอร์ พื้นฐานควอนตัมเมคานิกส์ ก็นั่งมาจาก d2(f(x))/dx2 = k*f(x) ซึ่งแก้ไปๆ มาๆ มันก็ออกมาพร้อมกับตัว e ทุกทีร่ำไป ผมจึงขออนุญาตปิดท้ายด้วย quote ใน คคห.10 อีกครั้งครับ "The most powerful force in the universe is compound interest" -Albert Einstein- ขอบคุณครับ แก้ไขเมื่อ 16 ส.ค. 52 12:55:37 จากคุณ : Little Humming Bug เขียนเมื่อ : 16 ส.ค. 52 12:35:41

ความคิดเห็นที่ 14   Taylor Series ครับ มันแตกอรุกรมออกมา แล้วไปหาที่นิยามของ e หรือค่าคงตัวครับ e = 1/ 1! + 1/2! + 1/3! http://en.wikipedia.org/wiki/E_(mathematical_constant) ก่อนนหน้านั้นก็จะเอา e ไปผูกกับ Sin Cos ผ่านทาง SinH CosH โดยความต่างของมัน คือ การใช้นิยามเชิงซ้อนเข้ามา แล้วก็ไปผูกกับ การหารากของ -1 = i ครับ มันผูกกันมาย้าว ยาว จากคุณ : ฟหกด เขียนเมื่อ : 16 ส.ค. 52 13:08:43 A:124.122.163.199 X: TicketID:205742

ความคิดเห็นที่ 15   เรื่องนี้จะต่อไปยัง laplace transform ต่อครับแล้วไปได้อีกเรื่อยๆ จากคุณ : ฟหกด เขียนเมื่อ : 16 ส.ค. 52 13:10:17 A:124.122.163.199 X: TicketID:205742

ความคิดเห็นที่ 16   นั่งอ่านแบบงงๆ สไตล์เด็กสายวิยาศาสตร์สุขภาพ จากคุณ : CuTTy 555 เขียนเมื่อ : 16 ส.ค. 52 15:42:32 A:118.172.63.254 X:

ความคิดเห็นที่ 17 มีคนตอบไปเยอะแล้ว ค่อนข้างจะเป็น math มากมายกันพอสมควร อยากจะตอบง่ายๆ ให้พอมองออก แล้วเกิดเป็นไอเดีย ถามว่า function e^x มายังไง ตอบแบบง่ายๆคือ มันวาปมา (ก็ตรูจะให้มันมีอ่ะ ใครจะทำไม) ถามว่า แล้วทำไมต้องมี เพราะว่า นักคณิตศาสตร์ ต้องการหาฟังชั่นอะไรซักอย่างที่ อนุพันธ์ของมัน เท่ากับตัวมันเอง แล้วหาได้ว่าเป็น e^x ถามว่า แล้วทำไมต้องหาฟังชั่นที่ f' = f ก็เพราะว่า อยากเอามาใช้งาน ที่จริงแล้วการหาฟังชั่นนี้ ไม่ใช่เรื่องลึกลับซับซ้อนอะไรเลย มันเหมือนกับ การหาค่าของ x ที่ cos(x) = x หรือหาค่าของ y ที่ log(y) = y หรืออื่นๆ หรือหาค่า sqrt(-1) = ค่า i ที่เราใช้กันอยู่ แต่ค่า x กับ y ที่หาได้จากตัวอย่างที่กล่าวไปนั้น มันไม่ได้มีประโยชน์อะไรในทางคณิตศาสตร์ เราเลยไม่พูดถึงมัน แต่  !!!! ฟังชั่นที่ดิฟแล้ว มีค่าเท่ากับตัวมันเอง  มีประโยช์อย่างยิ่ง ในทางคณิตศาสตร์ (calculus) ประโยชน์ยังไง ไม่ขอกล่าว เพราะคิดว่าถ้าท่านไปดู proof ของสูตรดิฟต่างๆท่านคงได้เห็นมาเยอะแล้ว ว่ามันต้องใช้ความพิเศษของฟังชั่นที่ ดิฟแล้วได้ตัวมันเอง (e^x) และจุดเด่นของ e^x คือ มันมีค่าเป็นจำนวนจริงในทุกๆค่าของ x นั่นคือ ถึงมันจะเป็นส่วนประกอบของสูตรต่างๆ แต่พอถึงที่สุดแล้ว เราสามารถแทนค่าออกมาให้เป็นจำนวนจริงได้ ซึ่งในจุดนี้จะแตกต่างกับค่า  i ที่เราต้องติดไว้ ถามว่า หาฟังชั่นนี้ยังไง ตอบว่า ผมก็ไม่รู้ ว่าความจริงเขาหากันยังไง แต่ถ้าจะหาแค่รูป curve มันก็ไม่ยาก ทำได้โดย วาดกราฟ ที่ความชันที่จุดใดๆ มีค่าเท่ากับค่าในแก่น y ของมันเอง ถ้าเราอดทนวาดไปเรื่อยๆ ก็จะได้ curve ของ e^x ออกมา แต่แค่นั้นมันไม่เพียงพอ เพราะเรารู้แค่รูปกราฟ แต่เรายังไม่รู้ฟังชั่น ที่จะแทนค่าเป็นจำนวนจริง ซึ่งผมก็ไม่ได้อ่านบทพิสูจน์ถึงที่มาของ e^x  แต่ถ้าจำไม่ผิด รู้สึกจะหาได้ในปี 18xx กว่าๆ ซึ่งแปลว่า ค่อนข้างเป็นเรื่องซับซ้อนพอสมควร  คิดว่าถ้าอยากรู้คงหาอ่านเพิ่มเติมได้ไม่ยาก จากที่กล่าวมา ถึงแม้ลำดับมันจะมั่วๆ ไม่ค่อยตรงกับเหตุการณ์จริง  แต่หวังว่าคงจะพอทำให้ท่านได้แนวคิดถึงความจำและที่มาของ e^x บ้างพอสมควร จากคุณ : ฉันมีค่าแค่ไหน เขียนเมื่อ : 16 ส.ค. 52 22:43:42

ความคิดเห็นที่ 18   http://en.wikipedia.org/wiki/E_(mathematical_constant) http://en.wikipedia.org/wiki/De_Moivre%27s_formula http://en.wikipedia.org/wiki/Euler%27s_identity จากคุณ : ฟหกด เขียนเมื่อ : 17 ส.ค. 52 03:01:26 A:124.120.217.83 X: TicketID:205742