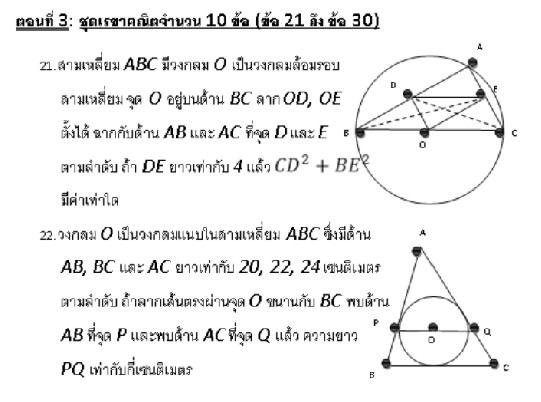
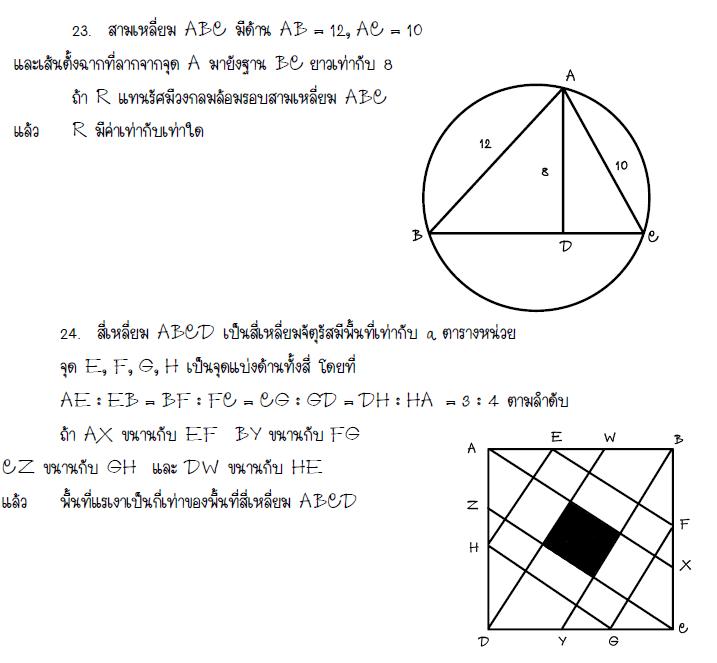
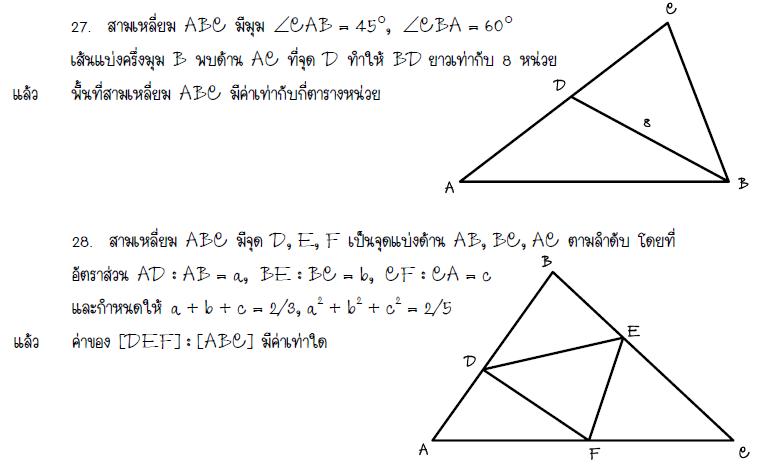
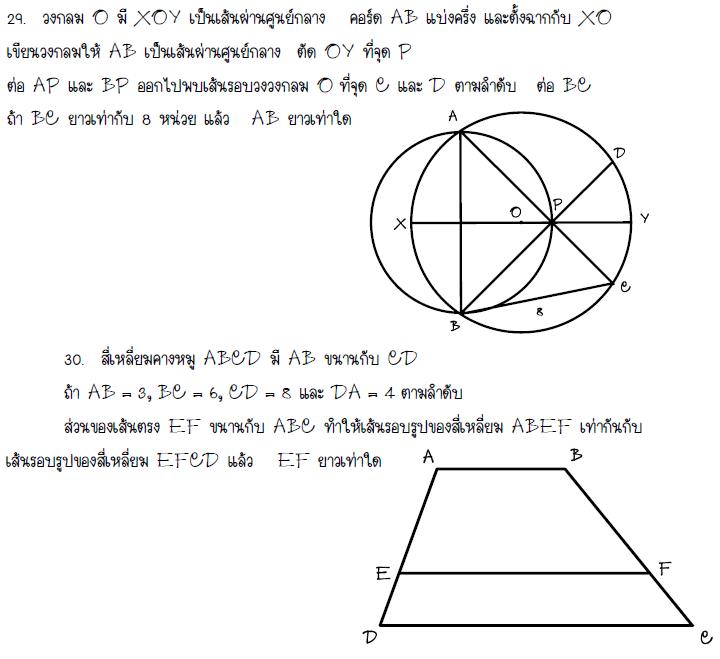
|
 ความคิดเห็นที่ 26
ความคิดเห็นที่ 26 |

ข้อ 12
สับเซตของ A มีทั้งหมด 212
ลบเซตว่างออกไปได้ 212-1
คราวนี้โจทย์ต้องการผลบวกของตัวมากสุดกับตัวน้อยสุดเท่ากับ 13 ทำไงดีหล่ะ???
แต่ตามหลักแล้วการมีอยู่ของมันต้องมีสัดส่วนที่คงตัวแน่
ลองสมมุติกรณีมี 3 ตัว {1,2,3}
จะมีสับเซตคือ เซตว่าง, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}
ผลบวกของตัวมากสุดกับตัวน้อยสุดเท่ากับ 4 มี 2 ตัว คือ {1,3}, {1,2,3}
ลองสมมุติกรณีมี 3 ตัว {1,2,3,4}
จะมีสับเซตคือ เซตว่าง, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}
,{1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}
ผลบวกของตัวมากสุดกับตัวน้อยสุดเท่ากับ 5 มี 5 ตัว คือ
{1,4}, {2,3}, {1,2,4}, {1,3,4}, {1,2,3,4}
เริ่มเห็นแนวโน้มการมีอยู่ของมันละมันมีประมาณ หนึ่งในสามของจำนวนสับเซตทั้งหมด
แต่หลังจากพิจารณาแล้วจะได้ว่า
ถ้ามีเซตAที่มีสมาชิค n ตัวแล้ว (โดยที่สมาชิกที่มีค่ามากสุดคือ z, สมาชิกที่มีค่าน้อยสุดคือ a)
ถ้า n เป็นเลขคู่แล้ว จำนวนสับเซต S ของ A โดยที่ผลบวกของสมาชิกที่น้อยสุดของ S
กับสมาชิกตัวที่มากที่สุดของ S เท่ากับ z-a เท่ากับ (2n-1)/3
ถ้า n เป็นเลขคี่แล้ว จำนวนสับเซต S ของ A โดยที่ผลบวกของสมาชิกที่น้อยสุดของ S
กับสมาชิกตัวที่มากที่สุดของ S เท่ากับ z-a เท่ากับ (2n-1)/3 ได้เศษเท่าไหร่ก็ตามให้ปัดลง
ดังนั้นคำตอบข้อนี้คือ (212-1)/3 = 1365
| จากคุณ |
:
jesus_god  
|
| เขียนเมื่อ |
:
31 ส.ค. 52 21:03:31
|
|
|
|
 |