|
 ความคิดเห็นที่ 10
ความคิดเห็นที่ 10 |

ต่อเนื่องจาก #9 นะครับ
-----------------------------------------------------------------------------
ค่าของ int (1/x) dx จาก x = 1 ถึง 101 กับค่าของ 1 + 1/2 + . . . + 1/100 ย่อมไม่เท่ากันอยู่แล้วครับ
(ในที่นี้ผมอินทิเกรตถึง 101 นะครับ โปรดดูเหตุผลข้างล่างครับ)
แต่ก็อาจมองว่าสองค่านี้พอจะเป็นค่าประมาณซึ่งกันและกันได้แบบหยาบๆ
(ซึ่งบังเอิญว่าค่อนข้างจะหยาบมากเสียด้วยครับ)
-----------------------------------------------------------------------------
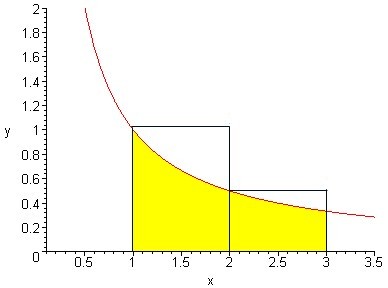
เหตุผลในเชิงรูปภาพคือ: (โปรดดูภาพข้างล่างประกอบ ซึ่งในภาพจะแสดงเฉพาะส่วนแรกๆ ของการหาค่านะครับ)
ค่าแรก int (1/x) dx จาก x = 1 ถึง 101 เป็นพื้นที่ใต้เส้นโค้ง y = 1/x จาก x = 1 ถึง 101 (ส่วนที่ระบายสีเหลือง)
ส่วนค่าที่สอง 1 + 1/2 + . . . + 1/100 = 1x1 + 1x1/2 + . . . + 1x1/100
เป็นผลรวมของพื้นที่รูปสี่เหลี่ยมผืนผ้าจำนวน 100 รูป
โดยแต่ละรูปมีฐานอยู่บนแกนนอน มีความกว้าง 1 หน่วย (จากจุด x ไป x+1) และสูง 1/x หน่วยเมื่อ x = 1, . . ., 100
(ผลบวกของพื้นที่รูปสี่เหลี่ยมผืนผ้าที่ว่านี้ ในทางแคลคูลัสเรียกว่า "ผลบวกบน" หรือ upper sum ครับ)
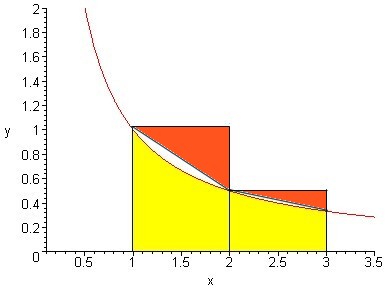
จากรูปข้างล่างจะเห็นว่าพื้นที่ของรูปสี่เหลี่ยมผืนผ้าแต่ละรูป จะเกินพื้นที่ใต้เส้นโค้ง (ส่วนสีเหลือง) ขึ้นไป
ส่วนที่เกินไปนี้ทำให้เกิด error ขึ้นครับ
-----------------------------------------------------------------------------
สรุปก็คือ การหาค่าของ 1 + 1/2 + . . . + 1/100 โดยหาจาก int (1/x) dx x = 1 ถึง 100 ก็จะมีความคลาดเคลื่อนเกิดขึ้นด้วยเหตุผลตามที่กล่าวมาครับ
แก้ไขเมื่อ 11 ก.ย. 52 19:05:07
| จากคุณ |
:
Accenda 
|
| เขียนเมื่อ |
:
11 ก.ย. 52 17:12:49
|
|
|
|
 |