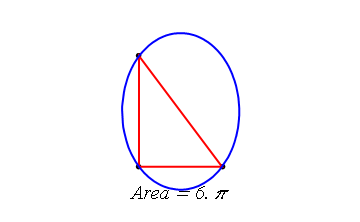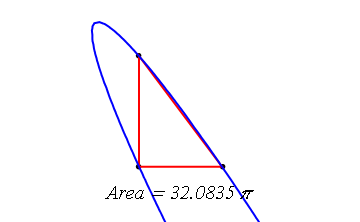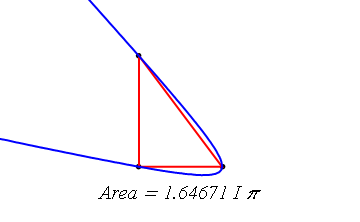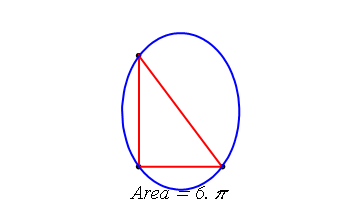 |
ความคิดเห็นที่ 3 |
พท.วงรี น้อยสุดที่ล้อมรอบ สามเหลี่ยมนี้คือ 6Pi
จากรูป เมื่อให้จุดทั้งสามมา เป็นพิกัดดังรูป
จุดทั้งสาม ทำให้ หาสมการวงรีได้คือ
(x-3/2)^2/a + (y-2)^2/b = 1
แทนค่า x,y = (0,0) จะได้ สมการ
9/4a^2 + 4/b^2 = 1
a = sqrt(9/(4(1 - 4/b^2)))
จาก พท.ของ วงรี = abPi
ab = bsqrt(9/(4(1 - 4/b^2)))
diff เทียบ b หาจุดต่ำสุด
(6 b)/sqrt(4 b^2-16)-(12 b^3)/(4 b^2-16)^(3/2) = 0
b = 0,-2sqrt(2),2sqrt(2)
ใช้ได้เฉพาะค่าบวก แทนค่า b หาค่า a ได้ a = 3/sqrt(2)
ดังนั้น พทวงรี = 6Pi ###
| จากคุณ |
:
mint_la  
|
| เขียนเมื่อ |
:
11 ม.ค. 53 01:06:18
|
|
|
|
|
