 |
ความคิดเห็นที่ 25 |
[เสริมเล็กน้อย]
เหตุที่ limn-->ฅ(1/n)ๅk=1n-1sin(kp/n)=๒01sinpx dx เพราะอะไร?
ก่อนอื่นดูรูปด้านล่างประกอบคำอธิบายก่อนครับ
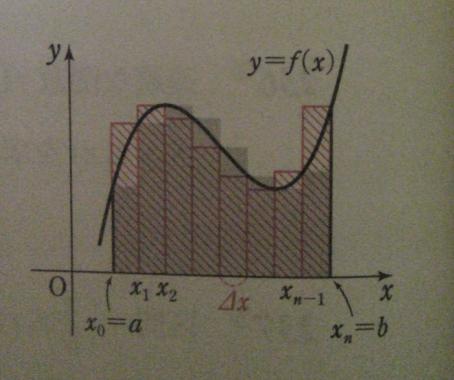
ฟังค์ชั่น f(x) ต่อเนื่องในช่วงปิด [a, b]. และในช่วงปิดนี้เราแบ่งเป็น n ส่วนเท่าๆกัน โดยที่ a=x0, x1, x2, ..., xn=b โดยที่ (b-a)/n = Dx จะได้ว่า xk = a + kDx จะได้ว่า
๒abf(x)dx = limn-->ฅๅk=0n-1f(xk)Dx = limn-->ฅๅk=1nf(xk)Dx
และถ้า a=0, b=1 จะได้ว่า Dx = 1/n, xk = k/n ก็จะได้ว่า
๒01f(x)dx = limn-->ฅ(1/n)ๅk=0n-1f(k/n) = limn-->ฅ(1/n)ๅk=1nf(k/n)
-----------------------------------------------------------------------------------------------------
ลองทำตามคำอธิบายด้านบนดู
ก่อนอื่นให้ S = limn-->ฅ(1/n)ๅk=1n-1sin(kp/n)
และ S = limn-->ฅ(1/n)ๅk=0n-1sin(kp/n) ด้วย เพราะ sin(0) =0
ดังนั้น S = limn-->ฅ(1/n)ๅk=0n-1sin(k*(p/n))
จึงเท่ากับ ๒01sinpx dx
| จากคุณ |
:
jesus_god   
|
| เขียนเมื่อ |
:
1 มี.ค. 53 06:26:30
|
|
|
|
|
