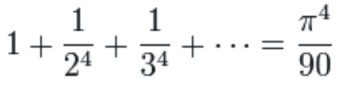|
 ความคิดเห็นที่ 14
ความคิดเห็นที่ 14 |

เวปนี้ใช้ได้ไหมครับ
http://mathforum.org/library/drmath/view/57128.html
ผมแปลออกนะ แต่บอกตรงๆ ไม่เข้าใจสักนิด
พวกโจทย์หาจำนวนเส้นทาง จำนวนขั้นตอน ผมตีความไม่เป็นครับ ต้องให้คนเก่งอธิบาย
You are correct that 0! = 1 for reasons that are similar to why
x^0 = 1. Both are defined that way. But there are reasons for these
definitions; they are not arbitrary.
You cannot reason that x^0 = 1 by thinking of the meaning of powers as
"repeated multiplications" because you cannot multiply x zero times.
Similarly, you cannot reason out 0! just in terms of the meaning of
factorial because you cannot multiply all the numbers from zero down
to 1 to get 1.
Mathematicians *define* x^0 = 1 in order to make the laws of exponents
work even when the exponents can no longer be thought of as repeated
multiplication. For example, (x^3)(x^5) = x^8 because you can add
exponents. In the same way (x^0)(x^2) should be equal to x^2 by
adding exponents. But that means that x^0 must be 1 because when you
multiply x^2 by it, the result is still x^2. Only x^0 = 1 makes sense
here.
In the same way, when thinking about combinations we can derive a
formula for "the number of ways of choosing k things from a collection
of n things." The formula to count out such problems is n!/k!(n-k)!.
For example, the number of handshakes that occur when everybody in a
group of 5 people shakes hands can be computed using n = 5 (five
people) and k = 2 (2 people per handshake) in this formula. (So the
answer is 5!/(2! 3!) = 10).
Now suppose that there are 2 people and "everybody shakes hands with
everybody else." Obviously there is only one handshake. But what
happens if we put n = 2 (2 people) and k = 2 (2 people per handshake)
in the formula? We get 2! / (2! 0!). This is 2/(2 x), where x is the
value of 0!. The fraction reduces to 1/x, which must equal 1 since
there is only 1 handshake. The only value of 0! that makes sense here
is 0! = 1.
And so we define 0! = 1.
| จากคุณ |
:
Firion  
|
| เขียนเมื่อ |
:
16 ก.ย. 53 23:47:33
|
|
|
|
 |






 ... เข้ามาดู
... เข้ามาดู