 |
 ความคิดเห็นที่ 9
ความคิดเห็นที่ 9 |

Addendum:
The above proof that 0!=1 is based upon n!=n(n-1)!, which is in turn based upon the definition of factorial. So, it would seem to be a valid proof. But, 0! cannot be defined directly from the definition of factorial. So, mathematicians like to define 0! as 1, without proving it. So, the proof just amounts to a demonstration that defining 0! as 1 is consistent with the definition of factorial.
I received email saying that my proof that 0!=1 is invalid because 0! is a constant, and you cannot solve for a constant. Wrong. I can find 4! (in a number of ways), and 4! is a constant. I can solve for the square root of 7, probably using my calculator, and it is a constant, too. There are numerous ways of finding pi, and it too is a constant.
n! is also the number of permutations (ways of arranging) exactly n things. It makes sense to say that there is one way to arrange zero things. So again, 0!=1.
| จากคุณ |
:
ชื่อนี้ได้มั้ยฮะ  
|
| เขียนเมื่อ |
:
17 ก.ย. 53 09:40:31
|
|
|
|
 |

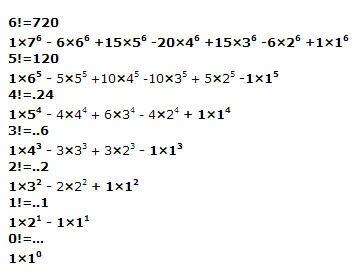


 ... เข้ามาดู
... เข้ามาดู