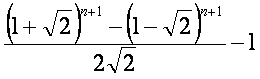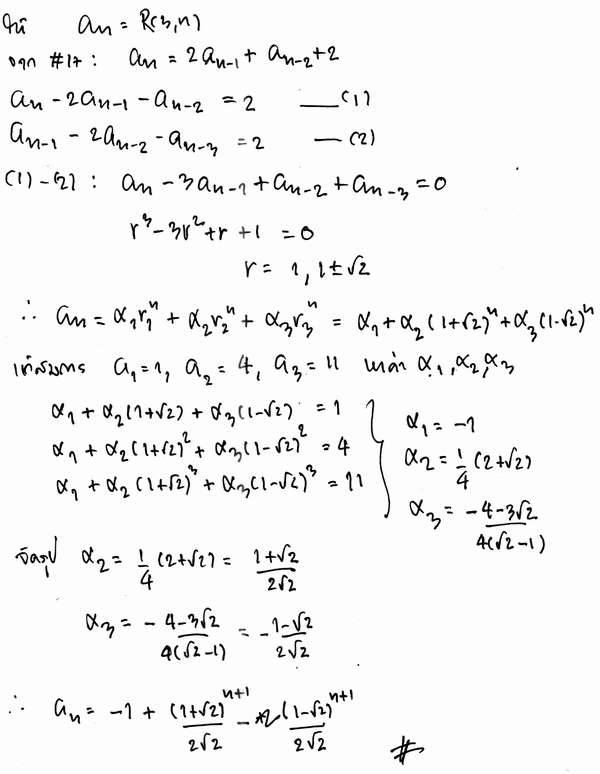 |
 
ความคิดเห็นที่ 17 |
วิธีคิดของโจทย์ข้อนี้ก็คือ
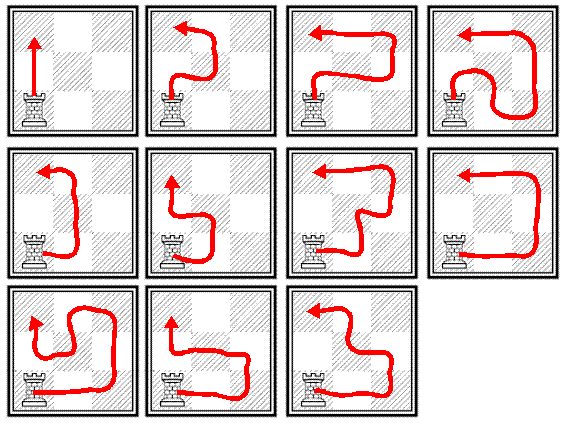
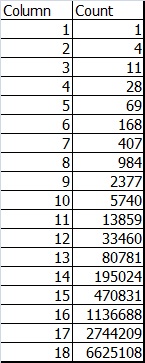
นับวิธีการ (3,1),(3,2) ไปเรื่อยๆ จนถึง (3,n)
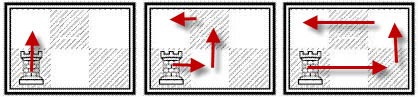
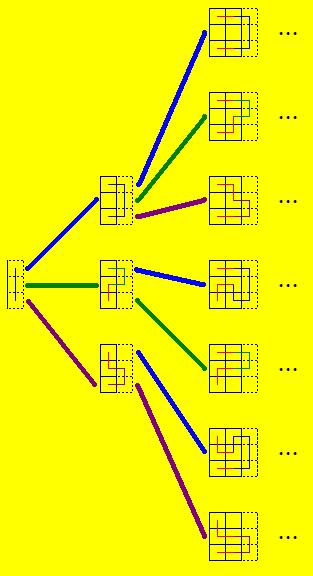
จากรูปเฉลย วิธี (3,1) จะมีวิธีเดียว
(3,1) จะแตกออกมาเป็น (3,2) ได้ 3 วิธี
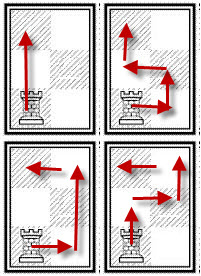
เส้นสีน้ำเงิน คือวิธีที่เส้นทางผ่านทั้ง 3 ช่องในคอลัมน์ท้าย
เส้นสีเขียว คือวิธีที่เส้นทางผ่านทุกช่องในคอลัมน์ท้ายยกเว้นช่องล่าง
เส้นสีม่วง คือวิธีที่เส้นทางผ่านทุกช่องในคอลัมน์ท้ายยกเว้นช่องบน
(3,2) แต่ละอัน จะแตกตามเฉพาะของแต่ละวิธี
วิธีการสีน้ำเงิน จะแตก (3,3) ออกมา 3 วิธีคือเส้นสีน้ำเงิน เขียว ม่วง
วิธีการสีเขียว จะแตก (3,3) ออกมา 2 วิธีคือเส้นสีน้ำเงิน เขียว
วิธีการสีม่วง จะแตก (3,3)ออกมา 2 วิธีคือเส้นสีน้ำเงิน ม่วง
แล้วที่แตกออกมา จะแตกตามวิธีของตัวเองไปอีกเรื่อยๆ
ถ้านับวิธีของ (3,n) ก็จะเป็นตาม Pn=2Pn-1+Pn-2; P1=1, P2=3
ก็จะได้ R(3,n) ว่า R(3,n)=2R(3,n-1)+R(3,n-2)+2; R(3,0)=0, R(3,1)=1
สรุปออกมา ก็ได้ตามรูปใน #6 ครับ
แต่จริงๆ ก็ search ใน oeis แบบ #15 นั่นแหละครับ
แก้ไขเมื่อ 18 ธ.ค. 53 20:31:42
| จากคุณ |
:
ABP@BDZ 
|
| เขียนเมื่อ |
:
18 ธ.ค. 53 20:23:58
|
|
|
|
|
