ความคิดเห็นที่ 1 โจทย์ข้อที่ 1 ปัญหา P vs NP แทบจะกล่าวได้ว่าเป็นปัญหาที่สำคัญที่สุดในวงการนักเขียนโปรแกรม เพราะโปรแกรมถึงจะดีขนาดไหน แต่ถ้าทำงานช้ายืดยาดเหลือเกิน ก็คงไม่มีใครอยากใช้ นักคอมพิวเตอร์จึงต้องจัดประเภทของรูปแบบของงานตามความเร็วที่คอมพิวเตอร์จะสามารถทำได้ "P" (Polynomial time) คือรูปแบบของงานที่คอมพิวเตอร์สามารถทำได้เร็ว "E" (Exponential time) คือรูปแบบของงานที่ต้องใช้เวลามาก อาจต้องใช้เวลาเป็นล้านๆปี แต่ รูปแบบงานทั่วไปของโรงงานอุตสาหกรรมห้างร้านทั้งหลาย ยากกว่าแบบ P แต่ก็ไม่ได้ยากเหมือนแบบ E จึงอยู่ตรงกลางและได้ชื่อว่ามีรูปแบบ "NP" (Nondeterministic Polynomial time) แต่ก็มีความเชื่อที่ว่างานในรูปแบบ NP นั้น ในความเป็นจริงอาจจะง่ายเหมือนอย่างงานในรูปแบบ P ก็ได้ เพียงแต่ยังไม่มีใครรู้วิธีเท่านั้นเอง ถ้าจะมีเครื่องคิดเลขสัก เครื่องแล้วคนคนหนึ่งอยากรู้ว่า 3329 คูณ 4547 ได้เท่าไหร่ กดเครื่องคิดเลขแปบเดียวก็ตอบได้แล้วว่าผลลัพท์คือ 15136963 แต่ในขณะเดียวกัน ถ้าจะมีคนอีกคนหนื่งอยากรู้ว่า 15136963 เท่ากับเลขใดคูณกัน เขาอาจต้องใช้เวลาเป็นวันๆในการกดเครื่องคิดเลขไล่ไปเรื่อยๆ การ "คูณ" นั้น สำหรับคอมพิวเตอร์แล้วเป็นงานที่ง่าย เป็นงานในรูปแบบ P แต่การ "แยกตัวประกอบ" นั้นเป็นงานที่ยาก เป็นงานในรูปแบบ NP แต่ทั้งนี้ ไม่มีใครแน่ใจว่า "งานที่ยาก" นั้น ยากโดยตัวของมันเอง หรือยากเพราะมนุษย์เรายังไม่รู้วิธีจัดการที่เหมาะสม ปัญหา P vs NP จึงเป็นเหมือนคำถามซ้อนคำถาม เพราะ P และ NP เองที่จริงก็คือรูปแบบของคำถามนี่เอง นักวิจัยส่วนที่เชื่อว่า P=NP จะพยายามหาวิธีแก้ปัญหาในรูปแบบ NP ให้เร็วขึ้น หากทำได้จริง คอมพิวเตอร์จะสามารถทำงานได้เร็วขึ้น ระบบอินเตอร์เนตและเครือข่ายสัญญาณทุกรูปแบบจะมีวิธีปรับปรุงใหม่ โรงงาน อุตสาหกรรมจะถูกออกแบบให้มีประสิทธิภาพมากขึ้น เส้นทางเดินเรือและระบบส่งสินค้าจะได้รับการพัฒนา เสน่ห์อย่างหนึ่ง ของโจทย์ปัญหาข้อนี้ก็คือ หาก P=NP จริง การพิสูจน์ว่า P=NP จะสามารถทำได้โดยใช้ความคิดสร้างสรรค์ล้วนๆไม่ต้องใช้คณิตศาสตร์เลย หากจะมีเด็กประถมสมองใส หาวิธีการทำงานหนึ่งงานใดในรูปแบบ NP-complete ให้เสร็จอย่างรวดเร็วได้ ก็จะได้ชื่อว่าพิชิตปัญหา P vs NP แล้ว จะอย่างไรก็ดี แม้แต่ผู้เชี่ยวชาญที่ทุ่มเทเวลาให้กับงานวิจัยก็ยังไม่พบวิธีแก้ปัญหาเหล่า นั้น จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 15:04:49

ความคิดเห็นที่ 2 โจทย์ข้อที่ 2 Poincare Conjecture ในปี 1904 พอย์นคาเร่ ได้ตีพิมพ์ผลงานวิจัยเกี่ยวกับ คุณสมบัติของรูปทรง และมิติสัมพันธ์ขึ้นมาฉบับหนึ่ง ในตอนท้ายของรายงายฉบับนั้น มีข้อติดข้องประการหนึ่งที่พอย์นคาเร่หาคำตอบไม่ได้ จนพอย์นคาเร่เสียชีวิต และนักคณิตศาสตร์หลายต่อหลายคนพยายามหาคำตอบให้กับปัญหานั้น แต่ไม่มีใครทำสำเร็จ ปัญหานั้นจึงได้รับการขนานนามว่า Poincare Conjecture แปลห้วนๆก็คือ ข้อคาดเดาของพอย์นคาเร่ นั่นเอง Poincare Conjecture เป็นคำถามเกี่ยวกับรูปทรงในสี่มิติ หากจะลองจินตนาการถึงผลส้ม ถ้าเอายางหนังสติ๊กไปรัดผลส้มไว้ ก็แน่นอนว่าหนังสติ๊กจะกระเด็นออกมาได้โดยที่ผลส้มยังคงทรงรูปร่างเดิม แต่หากจะจินตนาการใหม่ถึงโดนัท ถ้าเอายางหนังสติ๊กไปร้อยผ่านรูของโดนัทไว้ ก็เป็นไปไม่ได้ที่หนังสติ๊กจะกระเด็นออกมาโดยที่โดนัทยังทรงรูปร่างเดิม จึงกล่าวได้ว่าผลส้มและโดนัทมีความแตกต่างกันในเชิงมิติสัมพันธ์ ในสายตาของนักฟิสิกส์แล้ว มิติที่สี่ไม่ได้เป็นแค่จินตนาการไร้สาระ ลูกโลกมีลักษณะเป็นทรงกลมสามมิติ แต่เพราะเราซึ่งมีขนาดเล็กกว่าโลกมากและอาศัยอยู่บนพื้นผิวของโลก ในสมัยก่อนคนเราจึงเชื่อว่าโลกแบน จนต่อมานักดาราศาสตร์จึงได้คำนวนพิสูจน์ว่าโลกกลม ในทำนองเดียวกัน ก็มีความเป็นไปได้ว่าอันที่จริงจักรวาลอาจจะมีสี่มิติ แต่เพราะเราอาศัยอยู่บนพื้นผิวของจักรวาล จักรวาลจึงปรากฏกับเราว่ามีแค่สามมิติ จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 15:07:38

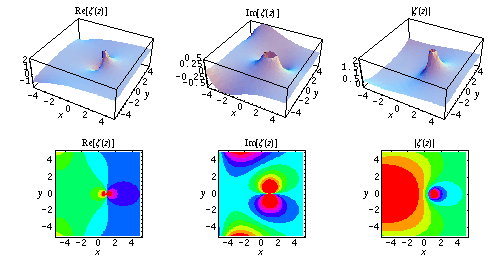
ความคิดเห็นที่ 3 โจทย์ข้อที่ 3 Riemann Hypothesis Riemann Hypothesis หรือสมมุติฐานของรีมันน์ อาจจะเป็นปัญหาที่อายุยืนที่สุดในเจ็ดข้อ และเป็นหนึ่งในปัญหาของฮิลเบอร์ ตในปี 1900 ที่หลงเหลือมาจนทุกวันนี้ ถ้าจะว่าให้เข้าใจง่ายที่สุด Riemann Hypothesis ก็เป็นโจทย์แก้สมการดีๆนี่เอง รีมันน์ได้ศึกษาฟังก์ชันตัวหนึ่งซึ่งมีชื่อว่า zeta function และมีนิยามบนจำนวนที่มากกว่า 1 ว่า zeta(s)=1/1^s+1/2^s+1/3^s+1/4^s+... zeta function นี้สามารถขยายนิยามออกไปได้แม้สำหรับค่า s ที่เป็นจำนวนเชิงซ้อน สิ่งที่รีมันน์สนใจในอันดับต่อไปก็คือ การหาค่า s ในสมการ zeta(s)=0 รีมันน์พบว่าสมการนี้มีคำตอบมากมายเหลือเกิน ตั้งแต่จำนวนเต็มลบคู่ทั้งหมด (ได้แก่ -2,-4,-6,...) และอีก "ส่วนหนึ่ง" ที่รีมันน์ไม่สามารถหาค่าได้หมด และไม่ทราบว่ามีอะไรบ้าง จะอย่างไรก็ดีนะครับ การแก้สมการดังกล่าวนี้ไม่ตรงไปตรงมาอย่างที่คิด เพราะเมื่อฟังก์ชันถูกขยายนิยามไปบนจำนวนเชิงซ้อนแล้วเรื่องประหลาดอาจเกิด ขึ้นได้มากมายไม่รู้จบ อย่างเช่น ฟังก์ชันเอกซ์โปเนนเชียลธรรมดาๆอย่าง e^x นั้น พอไปอยู่บนแกนจำนวนเชิงซ้อนแล้วจะกลับกลายเป็นฟังก์ชันตรีโกณมิติ ไป แต่ zeta function นี้ซ้ำร้ายยิ่งไปกว่านั้น บนจำนวนเชิงซ้อน zeta function จะไม่มีนิยามที่ตรงไปตรงมา แต่ต้องอาศัยฟังก์ชันอื่นๆอีก zeta function มีความสัมพันธ์โดยตรงกับจำนวนเฉพาะ (จำนวนที่แยกตัวประกอบไม่ได้ เช่น 2,3,5,7,11,13,17,19,23,29,...) ไม่มีใครรู้สูตรสำเร็จในการหาค่าจำนวนเฉพาะ แต่บทพิสูจน์ของ Riemann Hypothesis จะมีประโยชน์ในการศึกษาการกระจายตัวของจำนวนเฉพาะ หากจะถามว่าทำไมต้องศึกษาการกระจายตัวของจำนวนเฉพาะ? คำตอบก็คือเพราะจำนวนเฉพาะเป็นกระดูกสันหลังของระบบรหัสที่ใช้ในการสื่อสาร ทุกวันนี้ หากไม่มีการศึกษาเรื่องจำนวนเฉพาะมาก่อน อินเตอร์เนตจะไม่มีความปลอดภัยเลย อีเมลจะถูกแฮคได้ทุกเมื่อ ความลับของบริษัทจะถูกโจมตีเมื่อไหร่ก็ได้ คำถามล้านที่สามนี้ถามว่า จริงหรือไม่ที่คำตอบอีก "ส่วนหนึ่ง" ที่เหลือนั้นจะต้องเป็นจำนวนเชิงซ้อนที่มีส่วนจริง (real part) เท่ากับ 1/2 จนถึงทุกวันนี้ นักคณิตศาสตร์ได้ใช้ซุปเปอร์คอมพิวเตอร์หาคำตอบของสมการเป็นล้านๆค่าแล้ว แต่ก็ไม่พบค่าใดที่ขัดแย้งกับ Riemann Hypothesis แก้ไขเมื่อ 26 ม.ค. 54 15:45:24 แก้ไขเมื่อ 26 ม.ค. 54 15:35:49 จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 15:09:44

ความคิดเห็นที่ 4 โจทย์ข้อที่ 4 Navier-Stokes Equations ท่ามกลางปรากฏการณ์ธรรมดาๆอย่างเช่น กระแสน้ำในทะเล คลื่นจากท้ายเรือข้ามฟาก ควันธูปที่ลอยไปในอากาศ ทิศทางของก้อนเมฆ ก็ยังมีสิ่งที่นักวิทยาศาสตร์ไม่รู้ไม่เข้าใจแฝงอยู่เต็มไปหมด นักฟิสิกส์เชื่อว่า ท่ามกลางความยุ่งเหยิงและการเคลื่อนที่อย่างไม่เป็นระบบระเบียบของของเหลว และก๊าซทั้งหลายนั้น จะต้องมี "กฏ" บางอย่างที่สามารถอธิบายและพยากรณ์การเคลื่อนที่ที่ดูประหนึ่งว่าไม่มีทิศ ทางนั้นได้ คำตอบของ Navier-Stokes Equations จะเป็นที่มาของกฏนั้น คน ที่เรียนวิศวะและฟิสิกส์ในมหาวิทยาลัย อาจจะเคยเรียนวิชา fluid mechanics และปวดหัวกับการแก้ differential equation เพื่อหาอัตราการกระจายตัวของของเหลวหรือก๊าซมาแล้ว ในทำนองเดียวกัน Navier-Stokes Equations เป็นสมการดิฟฟีเรนเชียลที่อธิบายการเคลื่อนที่ของของไหล แต่มีเงื่อนไขมากมายและเขียนใหม่ได้หลายรูปแบบ จนถึงทุกวันนี้ แม้แต่ในเงื่อนไขที่ง่ายที่สุด ก็ยังไม่มีใครสามารถหาคำตอบของสมการดังกล่าวได้ ไม่มีใครสามารถบอกได้ว่าคำตอบมีหรือไม่มี และไม่มีใครสามารถบอกได้ว่าถ้ามีคำตอบ คำตอบนั้นจะมีคุณสมบัติอะไรบ้าง ในความเป็นจริงแล้ว คำตอบของ Navier-Stokes Equations มีความจำเป็นในการสร้างรถเรือและเครื่องบินที่มีความเร็วสูง นักวิศวกรจึงต้องอาศัยคอมพิวเตอร์หาคำตอบตามสถานการณ์เป็นครั้งๆไป Navier-Stokes Equations เป็นประหนึ่งน้องๆของทฤษฏีแห่งความยุ่งเหยิง คำตอบของสมการนี้จะเป็นประโยชน์อย่างมหาศาล กระแสน้ำและคลื่นลมจะได้รับการ อธิบาย การพยากรณ์อากาศจะแม่นยำมาก ระบบเตือนซึนามิและพายุจะมีประสิทธิภาพเพิ่มขึ้น จะมีรถและเครื่องบินยุคใหม่ แม้แต่ในวงการแพทย์ก็จะเข้าใจระบบไหลเวียนโลหิตดีขึ้น จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 15:14:53

ความคิดเห็นที่ 5 โจทย์ข้อที่ 5 Birch and Swinnerton-Dyer Conjecture Birch and Swinnerton-Dyer Conjecture เป็นปัญหาคณิตศาสตร์บริสุทธิ์เกี่ยวกับสมการหลายตัวแปรที่ต้องการคำตอบเป็น จำนวนเต็ม สมการที่ดูเหมือนง่ายๆนั้น ในบางกรณีก็ไม่มีคำตอบที่เป็นจำนวนเต็ม อย่างเช่น ไม่มีจำนวนเต็ม x และ y ใดๆ ที่ทำให้ x^2=4y+2 หรือที่โด่งดังกว่านั้นก็คือสมการ x^n+y^n=z^n สำหรับ n มากกว่า 2 ที่รู้จักกันในนาม Fermat's last theorem หรือ ทฤษฎีบทสุดท้ายของเฟอร์มาต์ ก่อน ที่เฟอร์มาต์จะเสียชีวิต เขาได้ทิ้งมรดกชิ้นสำคัญไว้ให้กับนักคณิตศาสตร์รุ่นหลังชิ้นหนึ่ง นั่นคือสมุดบันทึกสูตรและบทพิสูจน์ต่างๆที่เขาค้นพบในช่วงยังมีชีวิต Fermat's last theorem เป็นทฤษฎีบทสุดท้ายในสมุดบันทึกเล่มนั้น น่าเสียดาย เฟอร์มาต์ไม่ได้ทิ้งบทพิสูจน์ไว้ บอกเพียงแต่ว่าหน้ากระดาษไม่พอเขียนเท่านั้น แต่ผลปรากฏก็คือว่า ในยุคนั้นไม่มีใครเติมเต็มชิ้นส่วนที่หายไปนี้ได้ ทฤษฎีบทสุดท้ายของเฟอร์มาต์เป็นปัญหาคาใจของเหล่านักคณิตศาสตร์อยู่หลายชั่ว อายุคน เวลาผ่านไปร่วมสามร้อยปี จนในปี 1994 Andrew Wiles ก็สามารถพิสูจน์ทฤษฎีบทสุดท้ายของเฟอร์มาต์ได้ โดยพิจารณาสมการ x^n+y^n=z^n ด้วยความเป็นกราฟ และเรียกชื่อกราฟนั้นว่า elliptic curve และก็ด้วยเหตุนี้เอง elliptic curve จึงเป็นที่สนใจของบรรดาเหล่านักคณิตศาสตร์ และเป็นกุญแจสำคัญของ Birch and Swinnerton-Dyer Conjecture ถ้าให้ C เป็น elliptic curve, L(C,s) เป็น L-series ของ C, และ r เป็น rank ของ C บนจำนวนตรรกยะแล้วจะได้ว่า เทอมที่น้อยที่สุดจากการกระจาย L(C,s) ที่ s=1 ก็คือ c(s-1)^r จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 15:17:11

ความคิดเห็นที่ 6 คำถามข้อที่ 6 Yang-Mills Theory เป็นความจริงที่ว่าฟิสิกส์ขาดคณิตศาสตร์ไม่ได้ ถ้าไอน์สไตน์พูดแต่เพียงปากเปล่าว่าสสารก็คือพลังงาน และพลังงานก็คือสสาร แต่ไม่สามารถสรุปสมการ e=mc^2 ออกมาได้ ทุกวันนี้เราก็อาจจะยังหัวเราะเยาะให้กับความคิดที่ว่าสสารแปลรูปเป็นพลังงานได้ นิ วตันรู้ตัวว่างานของเขาต้องการเครื่องมือบางอย่างจากคณิตศาสตร์ ซึ่งเป็นเครื่องมือที่นักคณิตศาสตร์ในยุคนั้นไม่เคยคิดถึง ไม่สนใจ และไม่รู้จัก นิวตันจึงต้องประดิษฐ์เครื่องมือนั้นขึ้นมาเอง เครื่องมือนั้นได้ถูกเรียกว่า "แคลคูลัส" ซึ่งต่อมาก็ได้ถูกโอนเข้าสู่มือนักคณิตศาสตร์ ได้รับการวางรากฐานตามแบบฉบับของคณิตศาสตร์อย่างที่เห็นกันทุกวันนี้ แม้แต่ในยุคนี้สถานการณ์เดิมๆก็ไม่ได้หายไปไหน ปัญหาเกิดขึ้นเมื่อทฤษฎีทางฟิสิกส์ไม่มีทฤษฎีทางคณิตศาสตร์รองรับ Yang กับ Mills เป็นนักควอนตัมฟิสิกส์ที่ค้นพบปรากฏการณ์บางอย่างจากผลการทดลอง และ ยืนยันได้จากการจำลองสถานการณ์ด้วยคอมพิวเตอร์ แต่ Yang กับ Mills ไม่สามารถอธิบายสิ่งที่เขาค้นพบได้ด้วยสิ่งที่คณิตศาสตร์มี ไม่สามารถหาสูตรสำเร็จอย่าง e=mc^2 ออกมาอธิบายสิ่งที่พวกเขาค้นพบได้ ปัญหา ที่มีชื่อว่า Yang-Mills Theory ข้อนี้จึงต่างกับข้ออื่นตรงที่ โจทย์ไม่ได้เป็นคำถามสำเร็จรูปในเชิงคณิตศาสตร์ แต่โจทย์คือการเอาคณิตศาสตร์เข้าไปในที่ที่คณิตศาสตร์ไม่เคยเข้าไป โจทย์ไม่ ได้ถามว่าคำตอบของสมการคืออะไร แต่ถามว่าสมการที่นักฟิสิกส์ต้องการคำตอบคือสมการอะไร เหมือนกับที่ไอน์สไตน์พบสูตรพลังงานกับมวลสาร และเหมือนกับที่นิวตันวางรากฐานให้กับวิชาแคลคูลัส คำถาม ล้านที่หกก็คือ ให้วางระบบรากฐานในเชิงคณิตศาสตร์ให้เพียงพอ เพื่อที่จะพิสูจน์ได้ว่า Yang-Mills Theory มีจริง และ mass gap (อนุภาคที่มีคุณสมบัติพิเศษอย่างหนึ่งในควอนตัมฟิสิกส์) มีจริง จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 15:18:51

ความคิดเห็นที่ 7 คำถามข้อที่ 7 Hodge Conjecture ในบรรดาปัญหาทั้งเจ็ด Hodge Conjecture เป็นปัญหาที่เข้าใจยากที่สุดและอธิบายยากที่สุด แต่ทั้งนี้ไม่ได้เป็นเพราะ ว่า Hodge Conjecture ยากกว่าข้ออื่น แต่ Hodge Conjecture เป็นปัญหาเฉพาะทางที่ลงลึกไปในส่วนของคณิตศาสตร์ที่จินตนาการตามได้ยาก ไอเดียเริ่มต้นก็คือ ถ้าเรานำวัตถุมาทากาวแล้วแปะกันเราก็จะได้รูปทรงใหม่ นักคณิตศาสตร์จึงเริ่มศึกษารูปทรงในหลายมิติที่มาจากการนำรูปทรงที่มีมิติ ต่ำกว่ามาเชื่อมกัน (ฟังแล้วไม่น่าเชื่อ แต่กระดาษแค่ไม่กี่แผ่นแปะกันก็ เกิดเป็นรูปทรงสี่มิติที่ลึกลับซับซ้อนได้ และรูปทรงด้านบนก็เป็นหนึ่งใน ตัวอย่างที่ได้มาจากวิธีการนี้) เทคนิคดังกล่าวนี้ได้ถูกพัฒนาอย่างแพร่หลาย ในทุกๆด้าน จนถึงจุดที่วัตถุที่ถูกนำมาเชื่อมติดกันไม่จำเป็นต้องเป็นรูปทรงอีกต่อ ไป แต่เป็นวัตถุเชิงพีชคณิตที่มีชื่อว่า algebraic cycle วัตถุเชิงพีชคณิตนี้ไม่ได้อยู่ในระบบมิติกว้างยาวสูงที่จับต้องได้ แต่อยู่ในระบบมิติที่มีชื่อว่า projective algebraic variety คำ ถามล้านที่เจ็ดถามว่า จริงหรือไม่ ที่บน projective algebraic variety บนจำนวนเชิงซ้อน วัตถุใน Hodge class มาจากจากผสมกันแบบเส้นตรงในเชิงตรรกยะของ algebraic cycle ถึง แม้ว่า บทพิสูจน์ของ Hodge Conjecture อาจจะไม่ได้เป็นประโยชน์กว้างขวางแบบที่วาดภาพตามได้เหมือนปัญหาข้ออื่นๆ แต่การพัฒนาในสาขาวิชานี้จะเป็นประโยชน์ในวงการอุตสาห์กรรม การออกแบบ และภาพยนตร์แอนิเมชั่น จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 15:20:38

ความคิดเห็นที่ 8 ความรู้ที่เหลืออยู่ตอนนี้ แค่อ่านโจทย์ก็มึนล่ะ - -" จากคุณ : Houdini เขียนเมื่อ : 26 ม.ค. 54 15:24:50

ความคิดเห็นที่ 9 ส่วนโจทย์ที่ แก้ได้แล้วคือ โจทย์ ข้อ 2 นะครับ ใครที่กำลังนั่งเอาดินสอปากกาคิดข้อ 2 Poincare Conjecture อยู่ ให้หยุดทำได้แล้วครับ เพราะมีคนทำได้แล้ว เขาคนนั้น ชื่อ Dr. Grigoriy Perelman ชาวรัสเซีย แต่เขาไม่ไปรับตังค์ 1 ล้านดอลลาร์ และปฏิเสธการที่จะรับเหรียญ Millennium Prize ด้วย ส่วนใครที่อ่านโจทย์ยังไม่เข้าใจ  อย่าเพิ่งน้อยใจไปครับ เพราะคุณคือคนปกติธรรมดาทั่วไป คนส่วนใหญ่ในโลก ใครที่อ่านโจทย์เข้าใจบ้าง ไม่เข้าใจบ้าง คุณคือคนที่มีความรู้ความสามารถ ส่วนคนที่อ่านโจทย์แล้วเข้าใจ  คุณคงพร้อมแล้วสำหรับ 1 ล้านดอลลาร์ ข้อมูลที่มา  http://www.vcharkarn.com/varticle/38718 จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 15:28:08

ความคิดเห็นที่ 10 โจทย์ข้อสองกับข้อสามเคยปรากฏในการ์ตูนเรื่อง Q.E.D. ครับ สนุกมาก จากคุณ : ผู้วิเศษในเมืองแห่งความเหงา เขียนเมื่อ : 26 ม.ค. 54 15:30:49

ความคิดเห็นที่ 11 พาราโอ๊ะคุดาไซ จากคุณ : Tuey_re เขียนเมื่อ : 26 ม.ค. 54 15:38:18

ความคิดเห็นที่ 12 ผมโง่มากเลยนะเนี้ย อ่านโจทย์ ผมยังตีความไม่ได้เลยบางข้ออะ คนแปลจาก Eng มาไทยนี้สุดยอดเลย จากคุณ : NeoTokyo เขียนเมื่อ : 26 ม.ค. 54 15:39:33

ความคิดเห็นที่ 13 เข้ามาเวียนหัว.... จากคุณ : ไม่มีการศึกษา เขียนเมื่อ : 26 ม.ค. 54 16:00:55

ความคิดเห็นที่ 14 สรุปแล้ว Yang-Mills Theory คืออะไรเนี่ย บอกแค่ว่าบางอย่าง จากคุณ : ผีฟรีคิก เขียนเมื่อ : 26 ม.ค. 54 16:02:56

ความคิดเห็นที่ 15 เพื่อความสนุก โจทย์ข้อแรกมีคน submit เฉลยแล้วสองคนครับ คนแรกเป็นวิศวกรจาก HP ตอบว่า P ไม่เท่ากับ NP เป็นเด็ดขาด ส่วนคนทีสองเป็น อาจารย์มหาวิทยาลัยในรัสเซีย ตอบว่า ไงๆก็เท่ากัน เขียนโปรแกรมโชว์มาแล้วด้วยสองครั้ง สองคนนี่้ต้องหน้าแตกคนนึงละครับ ระหว่างนี้เราก็รอคณะกรรมการตรวจสอบ แล้วก็ถือหางเชียร์กันตามสะดวก :p จากคุณ : house (panote_saechiew) เขียนเมื่อ : 26 ม.ค. 54 16:10:35

ความคิดเห็นที่ 16 อุปมานของปวงคาเร่ สุดยอดมากอ่ะอ่านจบขนลุกเลย จากคุณ : ผีฟรีคิก เขียนเมื่อ : 26 ม.ค. 54 16:14:54

ความคิดเห็นที่ 17 ค.ห. 16 อย่างน้อยก็ช่วยอธิบายให้ฟังหน่อยครับ ว่าเค้าแก้ยังไง ใช้วิธีไหน  อย่างน้อยจะได้ร่วมขนลุกด้วยคน จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 26 ม.ค. 54 16:35:11

ความคิดเห็นที่ 18 โอย เด็ก MATH ยังมึน -__-! จากคุณ : Mea Culpa เขียนเมื่อ : 26 ม.ค. 54 19:51:07

ความคิดเห็นที่ 19 ข้อหนึ่งนี่คุ้นๆเหมือนตอนทำข้อสอบแล้วไม่รู้สมการ  เลยตั้งสมมุติฐานแล้วแทนค่าดู   พูดง่ายๆว่าคำตอบได้สองคะแนนส่วนวิธีทำได้ศูนย์ แก้คำผิด แก้ไขเมื่อ 26 ม.ค. 54 20:22:43 จากคุณ : fdX3S เขียนเมื่อ : 26 ม.ค. 54 20:22:12

ความคิดเห็นที่ 20 อ๋อ! ...อ่า...อืม...เอ่อ... แบ๊ะๆๆ จากคุณ : จันทร์เย็น เขียนเมื่อ : 26 ม.ค. 54 20:28:24

ความคิดเห็นที่ 21 ผมเล็งข้อ 3 กับ 7 อยู่ครับ ห้ามแย่งผมนะ 55+ โครตฝันเฟื่องเลย แต่บางข้อผมว่าให้นักฟิสิกส์แก้ดีกว่าครับ เพราะต้องใช้การทดลองด้วย จากคุณ : 123 เขียนเมื่อ : 26 ม.ค. 54 20:40:16 A:113.53.33.65 X: TicketID:300875

ความคิดเห็นที่ 22 อืมมม คุ้นๆกับ  Navier-Stokes Equations ตอนสมัยเรียน Aerodynamic กับ Gas Dynamic แต่ใส่โอ่งหินฝังดินไปเรียบร้อย เลาๆว่ายากมาก บางทีต้อง Trial and Error เอา ขนาดกำหนดค่าคงที่มาเพียบเลยนะ เอวังด้วยประการละฉะนี้ จากคุณ : Akysar เขียนเมื่อ : 26 ม.ค. 54 21:09:34

ความคิดเห็นที่ 23 อืมมม โอ้ววว อ้าาา เอ๋....เอ๋อ.....ปวดตับ จากคุณ : คุณแมวดำ เขียนเมื่อ : 26 ม.ค. 54 22:31:54

ความคิดเห็นที่ 24 งงทุกข้อ จากคุณ : icheerbank (icheerbank) เขียนเมื่อ : 26 ม.ค. 54 23:40:39

ความคิดเห็นที่ 25 โจทย์ ข้อ 8 สุดยอดคำถามคณิตศาสตร์แห่งศตวรรษ       จงพิสูจน์ว่า  1= 0.99999.... ตอบได้ รับไปเลย 1- 0.99999.... ล้านดอลลาร์ แก้ไขเมื่อ 27 ม.ค. 54 02:24:23 แก้ไขเมื่อ 27 ม.ค. 54 02:16:33 จากคุณ : Peterfly (peterfly) เขียนเมื่อ : 27 ม.ค. 54 02:15:02

ความคิดเห็นที่ 26 จขกท.  ก็ มึน ทุกข้อเหมือนกันครับ   จากคุณ : คนสร้างภูเขา เขียนเมื่อ : 27 ม.ค. 54 07:50:18

ความคิดเห็นที่ 27 นอกจากข้อ 1 แล้ว ข้ออื่น อ่าน จบแล้ว ยังไม่รู้เลยว่าถามอะไร จากคุณ : mangginoon เขียนเมื่อ : 27 ม.ค. 54 08:50:50

ความคิดเห็นที่ 28 ผมชอบข้อสามน่ะ จากคุณ : Santa_Baby เขียนเมื่อ : 27 ม.ค. 54 09:54:43

ความคิดเห็นที่ 29 ************ ในสายตาของนักฟิสิกส์แล้ว มิติที่สี่ไม่ได้เป็นแค่จินตนาการไร้สาระ ลูกโลกมีลักษณะเป็นทรงกลมสามมิติ แต่เพราะเราซึ่งมีขนาดเล็กกว่าโลกมากและอาศัยอยู่บนพื้นผิวของโลก ในสมัยก่อนคนเราจึงเชื่อว่าโลกแบน จนต่อมานักดาราศาสตร์จึงได้คำนวนพิสูจน์ว่าโลกกลม ในทำนองเดียวกัน ก็มีความเป็นไปได้ว่าอันที่จริงจักรวาลอาจจะมีสี่มิติ แต่เพราะเราอาศัยอยู่บนพื้นผิวของจักรวาล จักรวาลจึงปรากฏกับเราว่ามีแค่สามมิติ ************* ตีความคร่าว ๆ นะครับ ตอนที่มนุษย์เรายังไม่ได้ออกจากโลก คิดว่าเป็น 2D พอออกนอกโลกได้ จึงบอกว่าเป็น 3D ฉะนั้นเลยสันนิฐานว่า ถ้าออกไปนอกจักรวาลอื่นได้ มันน่าจะเป็น 4D ใช่ใหม ผมว่าตรงนี้มันแมร่ง ๆ นะครับ ต่อให้โลกแบนหรือกลม มันก็ยังเป็น 3D อยู่นิ แล้วการที่จะพิสูจน์ 4D มันจะพิสูจน์ได้อย่างไร ปล. เหมือนหนังไซไฟ Island เลย ส่วนตัวคิดว่ามันไม่น่าจะจริงอย่างมาก จากคุณ : หางอึ่งน้อยนิด (Bearlandia) เขียนเมื่อ : 27 ม.ค. 54 10:36:59

ความคิดเห็นที่ 30 โอ๊ย ปัญหาทั้งหมดนี้มันก็มีคำตอบอยู่ในเรื่อง Fractral นั่นเอง จากคุณ : kongp (kongp) เขียนเมื่อ : 27 ม.ค. 54 14:00:50

ความคิดเห็นที่ 31 ปวดหัวเลย == จากคุณ : GigglEAuN เขียนเมื่อ : 28 ม.ค. 54 21:26:05

ความคิดเห็นที่ 32 #4 แก้ได้เมื่อไร ลูกกระสุนคงยิงเป็นวิถีโค้งได้เหมือนในหนังจริงๆ จากคุณ : .. (MoonClock~*) เขียนเมื่อ : 29 ม.ค. 54 16:18:00

ความคิดเห็นที่ 33 เห็นโจทย์ทั้งหมดนี้แล้วผมขอเวลา 3 วัน ปล.ขอเวลาพักสมองแล้วมาอ่านต่อนะ จากคุณ : โอไซริส เขียนเมื่อ : 29 ม.ค. 54 18:24:30