|
สงสัยจะมาตอนตลาดวายซะแล้ว
ลักษณะโจทย์แบบนี้(ถ้าโจทย์ไม่ผิด) มันบอกเราเป็นนัยๆว่า
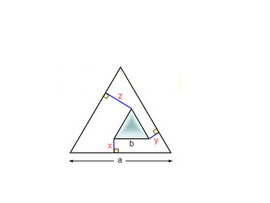
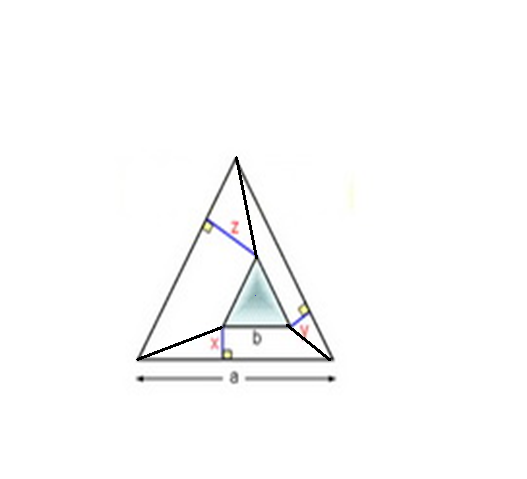
ไม่ว่าสามเหลี่ยมเล็กจะอยู่ตำแหน่งใดภายในรูปสามเหลี่ยมใหญ่ก็ตาม
ค่าของx+y+z จะเท่ากับค่าคงที่ค่าหนึ่งเสมอ
เพราะงั้นเราแอบขี้โกงจับสามเหลี่ยมเล็กไปอยู่ตำแหน่งไหนภายในรูปสามเหลี่ยมใหญ่ก็ได้ที่จะทำให้เราคิดเลขง่ายขึ้น
หรือจะกำหนดขนาดของรูปสามเหลี่ยมเอาเองตามแบบ คห บนๆก็ได้คำตอบที่ถูกเหมือนกันคับ
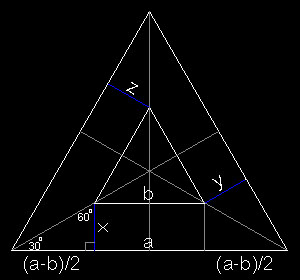
แต่จริงๆแล้วเราสามารถแสดงได้ว่า x+y+z = 3/2 เสมอตามนี้คับ
จากรูป
พื้นที่ของสามเหลี่ยมใหญ่ = พื้นที่สามเหลี่ยมเล็ก + พื้นที่สี่เหลี่ยมคางหมู3รูป
สูตรพื้นที่สามเหลี่ยมด้านเท่า >>> (sqrt(3) ด้าน^2)/4
สูตรพื้นที่สี่เหลี่ยมคางหมู >>> (1/2)*ผลบวกด้านคู่ขนาน*สูง
แทนค่า
(sqrt(3)a^2)/4 = (sqrt(3)b^2)/4 + (1/2)(a+b)X + (1/2)(a+b)Y + (1/2)(a+b)Z
(sqrt(3)/4)(a^2 - b^2) = (1/2)(a+b)(X+Y+Z)
(sqrt(3)/4)(a+b)(a-b) = (1/2)(a+b)(X+Y+Z)
(sqrt(3)/4)sqrt(3) = (1/2)(X+Y+Z) ; แทนค่า a-b = sqrt(3) , a+b ตัดกัน
X + Y + Z = 3/2
| จากคุณ |
:
อิอิคุง  
|
| เขียนเมื่อ |
:
4 มิ.ย. 54 00:08:41
|
|
|
|
 |