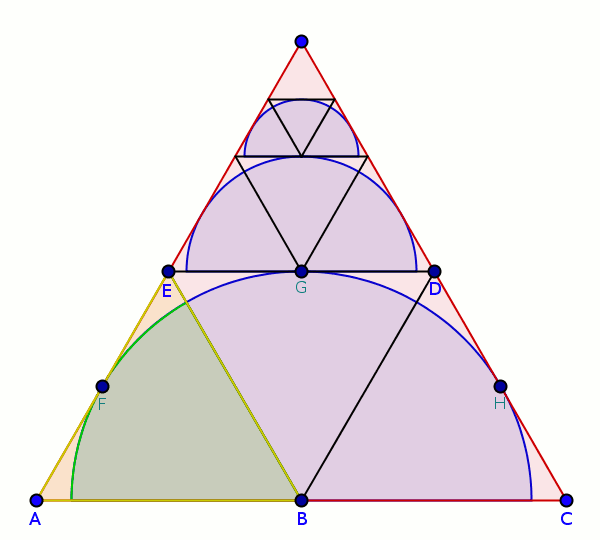
 |
∠BAE = ∠BCD = 60°
△BEF,△BEG,△BDG,△BDH เท่ากันทุกประการ
∠BEF = ∠BEG = ∠BDG = ∠BDH
∠BEA = ∠BED = ∠BDE = ∠BDC
สี่เหลี่ยม ACDE มีมุมภายในรวมกัน 360°
∠EAC + ∠ACD + ∠CDE + ∠DEA = 360°
60° + 60° + (∠BDC + ∠BDE) + (∠BED + ∠BEA) = 360°
4*(∠BEA) = 240°
∠BEA = 60°
∠BEA = ∠BED = ∠BDE = ∠BDC = 60°
△ABE,△BED,△BDC เป็นสามเหลี่ยมด้านเท่า
สังเกตว่า รูปทั้งหมดนี้ประกอบด้วย ส่วนที่เราจะคิดพื้นที่เป็น sector60° ที่บรรจุในสามเหลี่ยมด้านเท่า ซึ่งมีขนาดต่างๆ กัน จำนวนมาก
พื้นที่่ครึ่งวงกลมทั้งหมดรวมกัน/พื้นที่สามเหลี่ยมทั้งหมด = พื้นที่ sector 60° ที่บรรจุในสามเหลี่ยมด้านเท่า/พื้นที่สามเหลี่ยมด้านเท่า
พื้นที่่ครึ่งวงกลมทั้งหมดรวมกัน = (พื้นที่ sector 60° ที่บรรจุในสามเหลี่ยมด้านเท่า/พื้นที่สามเหลี่ยมด้านเท่า) * พื้นที่สามเหลี่ยมทั้งหมด
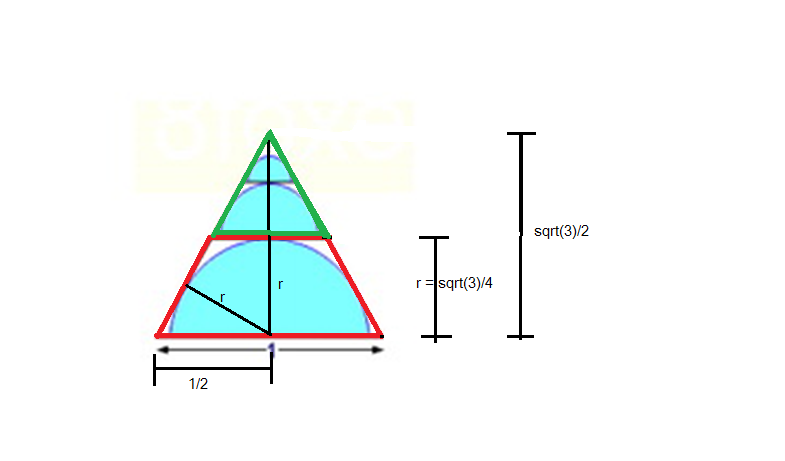
พื้นที่สามเหลี่ยมทั้งหมด = พื้นที่สามเหลี่ยมด้านที่มีด้านยาวด้านละ 1 หน่วย
พื้นที่่ครึ่งวงกลมทั้งหมดรวมกัน = (พื้นที่ sector 60° ที่บรรจุในสามเหลี่ยมด้านเท่า/พื้นที่สามเหลี่ยมด้านเท่า) * พื้นที่สามเหลี่ยมด้านที่มีด้านยาวด้านละ 1 หน่วย
พื้นที่ครึ่งวงกลมทั้งหมดรวมกัน = พื้นที่ sector60° ที่บรรจุในสามเหลี่ยมด้านเท่า ที่มีด้านยาวด้านละ 1 หน่วย
= pi * (sqrt(3)/2)^2 * 60/360 = pi/8
| จากคุณ |
:
ผลึกความคิด  
|
| เขียนเมื่อ |
:
6 มิ.ย. 54 17:50:06
|
|
|
|
|
ผลรวมพื้นที่ครึ่งวงกลมทั้งหมดเท่ากับเท่าไหร่ครับ?
