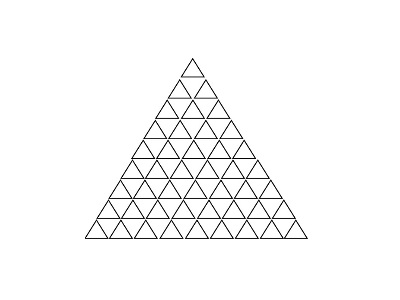
 |
สามเหลี่ยมด้านเท่า จะมีอยู่2แบบหลักๆคือ แบบหงาย และแบบคว่ำ
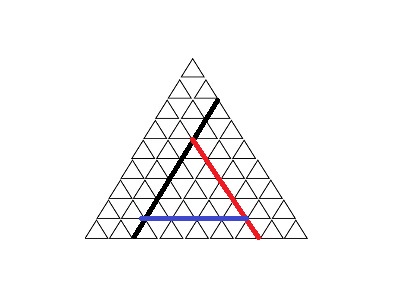
สำหรับแบบหงาย จะเกิดจากเส้นสามรูปแบบคือ เส้นดำ(เส้นที่เฉียงขึ้นไปทางขวา) เส้นแดง(เส้นที่เฉียงขึ้นไปทางซ้าย) และเส้นน้ำเงิน(เส้นนอน) ดังรูป
ต่อไปนี้เพื่อความเข้าใจตรงกัน เราจะเรียกเส้นที่เฉียงขึ้นไปทางขวาว่าเส้นดำ ,เรียกเส้นที่เฉียงขึ้นไปทางซ้ายว่าเส้นแดง , เรียกเส้นนอนว่าเส้นน้ำเงิน
จากรูปจะเห็นว่ามีเส้นดำอยู่9เส้น
ให้ A(i) แทนจำนวนสามเหลี่ยมด้านเท่าทั้งหมดที่เกิดจากการเลือกเส้นดำที่ i (นับจากเส้นซ้ายสุด)
จะได้ว่า จำนวนรูปสามเหลี่ยมด้านเท่าแบบหงาย = ๅ A(i) ; i=1ถึง i=9
เมื่อเราเลือกเส้นดำเส้นที่ i แล้ว เราสามารถเลือกเส้นแดงได้อีก 10 - i เส้น
ให้ B(k) แทนจำนวนสามเหลี่ยมด้านเท่าทั้งหมดที่เกิดจากการเลือกเส้นแดงเส้นที่ k (เมื่อนับจากเส้นที่ติดกับเส้นดำเส้นที่iไปจนเส้นดำขวาสุด)
จะได้ว่า A(i) = ๅ B(k) ; k =1 ถึง k = 10-i
เมื่อเราเลือกเส้นแดงเส้นที่ k แล้วเราสามารถเลือกเส้นน้ำเงินได้ k เส้นพอดี นั่นคือ B(k) = k
ดังนั้นจำนวนรูปสามเหลี่ยมด้านเท่าแบบหงาย = ๅ A(i)
= ๅ [ๅ B(k)]
= ๅ [ๅ k]
= 165
| จากคุณ |
:
อิอิคุง  
|
| เขียนเมื่อ |
:
วันต่อต้านยาเสพติดโลก 54 13:42:37
|
|
|
|
|
ช่วยนับหน่อยครับมีสามเหลี่ยมด้านเท่าทั้งหมดกี่รูป?
