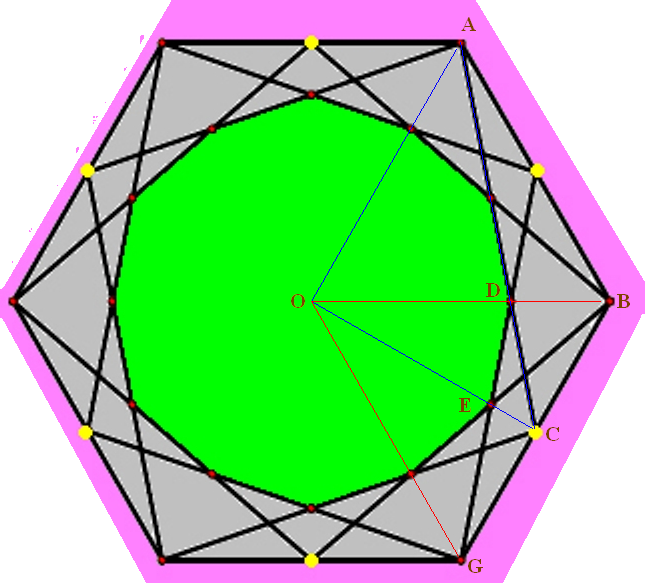
 |
๑. จากโจทย์ แต่ละเส้นสมมาตรกัน ดังนั้นพื้นที่สีเขียว จะเป็นรูปสิบสองเหลี่ยมด้านเท่า มุมเท่า
๒. พิจารณาแค่สามเหลี่ยมมุมฉาก AOC จะได้ OA = 1 หน่วย (เท่ากับด้านของหกเหลี่ยม) และ OC = (รูท3)/2 หน่วย (ส่วนสูงของสามเหลี่ยมด้านเท่า GOB)
๓. ดังนั้น AC = รูท(OA2+OC2) = (รูท7)/2
๔. ทำให้ได้ sin (OAC) = OC/AC = (รูท3)/(รูท7) และ cos (OAC) = OA/AC = 2/(รูท7)
๕. พิจารณาเฉพาะสามเหลี่ยม OAD จะได้ มุม AOD = 60 องศา, มุม ODA = 180 - 60 - A = 120 - A องศา (A คือ มุม OAD)
๖. หา OD โดยใช้กฎของไซน์ OD/sin(OAD) = OA/sin(ODA) ดังนั้น OD = sin(OAD)/sin(ODA) เนื่องจาก OA = 1 ก็เลยสบาย 555
๗. หาค่า sin(ODA) = sin(120 - A) = sin 120 cos A - cos 120 sin A = (รูท3)(cos A)/2 + (sin A)/2
แทนค่า cos A กับ sin A ที่ได้จากข้อ ๔. จะได้
๘. sin(ODA) = (3รูท3)/(2รูท7)
หา OD จาก ข้อ ๖. ต่อ โดย แทนค่า sin(OAD) จากข้อ ๔. จะได้
๙. OD = sin(OAD)/sin(ODA) = (รูท3)/(รูท7) หารด้วย (3รูท3)/(2รูท7) = 2/3
๑๐. คำนวณหาพื้นที่สามเหลี่ยม ODE (รู้ว่ามุม DOE = 30 องศา เพราะเป็นครึ่งหนึ่งของมุม GOB)
พท.สามเหลี่ยม ODE = (1/2)(sin 30)(OD)(OE) = (1/2)(1/2)(2/3)(2/3) = 1/9
พท.สีเขียว = สามเหลี่ยม ODE สิบสองรูป = 12/9 = 4/3 ตารางหน่วยครับ
ถูกรึเปล่าครับ
| จากคุณ |
:
basicguy 
|
| เขียนเมื่อ |
:
18 ก.ค. 54 01:01:04
|
|
|
|
|
พ.ท. สีเขียวเท่ากับเท่าไหร่ครับ???
