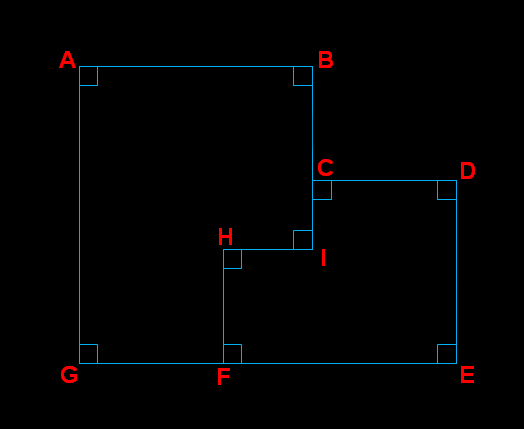
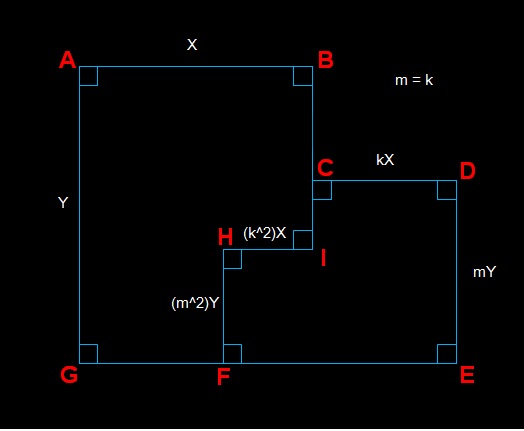
 |
ให้ความยาวด้านAB = X และ ความยาวด้านAG = Y
สมมติว่าด้านCDมีความยาวเป็น k เท่าของด้านAB
และด้านDEมีความยาวเป็น m เท่าของด้านAG
จะได้ ความยาวด้านCD = kX และ ความยาวด้านDE = mY และจะได้ความยาวEG = X + kX = (k+1)X
เนื่องจากรูปหลายเหลี่ยม ABCDEG และรูปหลายเหลี่ยม CDEFHI คล้ายกัน
จะได้ว่า AB / CD = AG / DE >>> X / (kX) = Y / (mY) >>> k = m
ดังนั้น ความยาวด้านCD = kX และ ความยาวด้านDE = kY และจะได้ความยาวBC = Y - kY = (1-k)Y
เนื่องจากรูปหลายเหลี่ยม ABCDEG และรูปหลายเหลี่ยม CDEFHI คล้ายกัน
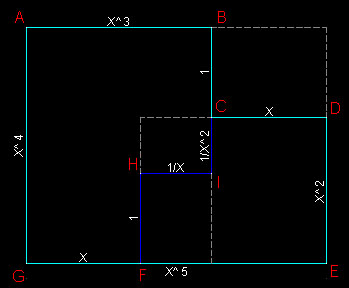
เมื่อด้านCDมีความยาวเป็น k เท่าของด้านAB และด้านDEมีความยาวเป็น k เท่าของด้านAG
จะได้ว่าด้านHIต้องมีความยาวเป็น k เท่าของด้านCD และด้านHFต้องมีความยาวเป็น k เท่าของด้านDEด้วย
นั่นคือ ความยาวด้านHI = k2X และ ความยาวด้านHF = k2Y
ความยาวด้านBI = Y - k2Y = (1-k2 )Y , ความยาวด้านGF = X - k2 X = (1-k2 )X
เนื่องจากรูปหลายเหลี่ยม ABCDEG และรูปหลายเหลี่ยม ABIHFG คล้ายกัน
เมื่อด้านCDมีความยาวเป็น k เท่าของด้านAB
จะได้ว่าด้านHFต้องมีความยาวเป็น k เท่าของด้านBI ด้วย
นั่นคือ k2 Y = k(1-k2 )Y >>> k2 +k-1 = 0 >>> k = (sqrt(5) - 1)/2
เนื่องจากรูปหลายเหลี่ยม ABCDEG และรูปหลายเหลี่ยม ABIHFG คล้ายกัน
จะได้ว่า AB / BI = AG / AB >>> X / ((1-k2 )Y) = Y / X >>> X = sqrt(1-k2 )Y
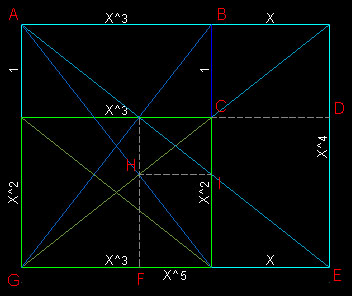
ดังนั้น BC : CD : DE : AB : AG : EG = (1-k)Y : kX : kY : X : Y : (k+1)X
= (1-k)Y : sqrt(1-k2 )kY : kY : sqrt(1-k2 )Y : Y : (k+1)sqrt(1-k2 )Y ; แทน X ด้วย sqrt(1-k^2)Y
= 1-k : sqrt(1-k2 )k : k : sqrt(1-k2 ) : 1 : (k+1)sqrt(1-k2 )
= k2 : k3/2 : k : sqrt(k) : 1 : 1/sqrt(k) ; 1-k2 = k และ k+1 = 1/k
= 1 : 1/[k1/2] : 1/k : 1/[k3/2] : 1/[k2] : 1/[k5/2 ] เมื่อ k = (sqrt(5) - 1)/2 ###
ได้ตรงกับ #1 ครับ
| จากคุณ |
:
อิอิคุง  
|
| เขียนเมื่อ |
:
22 ส.ค. 54 16:39:12
|
|
|
|
|
อัตราส่วน BC : CD : DE : AB : AG : EG เป็นเท่าไหร่ครับ???
