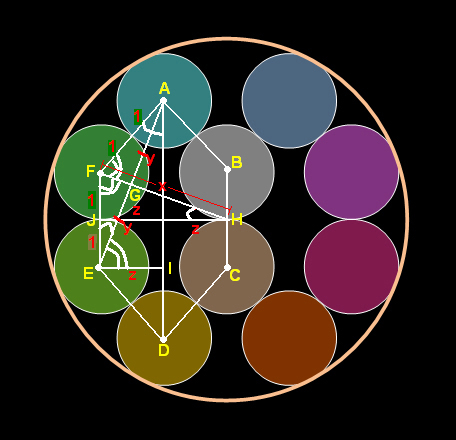
|
ให้รัศมีของวงกลมใหญ่ = R หน่วย และKเป็นจุดศูนย์กกลางของวงกลมใหญ่
จากรูปจะเห็นได้ชัดว่า ความยาวkf = ความยาวke = ความยาวkd = ความยาวkc = R-1 หน่วย
กำหนดให้ ความยาวae = ความยาวbd = x หน่วย
จะได้ ความยาวeg = ความยาวdh = x/2 หน่วย
และจากปิธากอรัสจะได้ว่า ความยาวgf = hc = sqrt(4-x2/4)
พิจารณาพื้นที่ของหกเหลี่ยมabcdefซึ่งหาได้2แบบดังนี้
พื้นที่ของหกเหลี่ยมabcdef = พื้นที่สี่เหลี่ยมabed + พื้นที่สามเหลี่ยมaef + พื้นที่สามเหลี่ยมbcd
= 2x + [x/2]sqrt(4-x2/4) + [x/2]sqrt(4-x2/4)
= 2x + x sqrt(4-x2/4) _______(1)
พื้นที่ของหกเหลี่ยมabcdef = พื้นที่สามเหลี่ยมafk + พื้นที่สามเหลี่ยมbck + พื้นที่สามเหลี่ยมfek + พื้นที่สามเหลี่ยมdek + พื้นที่สามเหลี่ยมdck
= 2[พื้นที่สามเหลี่ยมafk] + 3[พื้นที่สามเหลี่ยมdek]
= x/2 + 3x _______(2)
จากสมการ(1)และสมหาร(2)จะได้ว่า
2x + x sqrt(4-x2/4) = x/2 + 3x >>> x = sqrt(7)
จากสามเหลี่ยมdekและปิธากอรัสจะได้ว่า
ความยาวek = sqrt(1+x2) = sqrt(1+(sqrt(7))2) = sqrt(8)
ดังนั้น R - 1 = sqrt(8) >>> R = 1+sqrt(8) ###
| จากคุณ |
:
อิอิคุง  
|
| เขียนเมื่อ |
:
25 ส.ค. 54 13:47:49
|
|
|
|
รัศมีของวงกลมวงใหญ่ เท่ากับเท่าไหร่ครับ???
