|
ผมขอแก้ใหม่ R/r = sqrt ของ [2+ sqrt(5)] หรือ ~2.058171027
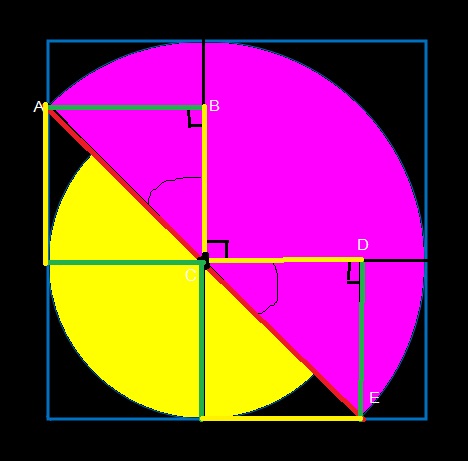
โดยที่ผมคำนวณจากพิธากอรัสดังนี้ (อ้างอิงจากรูปความเห็นที่ 3)
ความยาวของเส้นสีเขียว = sqrt (R2-r2) (ใช้พิธากอรัสคำนวณ)
ความยาวของเส้นสีเขียว + เส้นสีฟ้า(ซึ่งเท่ากับ r) เท่ากับด้านของสามเหลี่ยม (สมมุติเท่ากับ a และ b)
ส่วนความยาวของด้านยาวของสามเหลี่ยม (สมมุติิเป็น c) เท่ากับ 2R
ดังนั้นจากกฏของพิธากอรัส c^2 = a^2 + b^2
แทนค่าได้
4R^2 = (r+ sqrt(R2-r2)^2 + (r+ sqrt(R2-r2)^2
หลังจากจัดเรียงสมการใหม่จะได้
R^2 = 2r x sqrt(R^2 - r^2)
เนื่องจากเราต้องการทราบอัตราส่วนของ R/r (นั่นคือเมื่อ r = 1)
แทนค่า r=1 ในสมการข้างบนจะได้
R^2 = 2 x sqrt(R^2 - 1)
ถ้ายกกำลังสองทั้งสองข้างจะได้
R^4 = 4(R^2 - 1)
R^4 - 4R^2 +1 = 0 ถึงตรงนี้ก็น่าจะแก้สมการได้แล้วนะครับ
วิธีนี้จะไม่ต้องใช้ข้อสรุปที่ว่า มุมตามความเห็นข้างบนเท่ากับ 45 องศา เนื่องจาก r (เส้นสีส้ม) อาจจะยาวไ่ม่เท่าเส้นสีเขียว
ผมไม่รู้ว่าวิธีนี้ถูกหรือเปล่า เพราะผมเป็นมือสมัครเล่น ให้ผู้รู้มาช่วยเช็คอีกทีครับ
| จากคุณ |
:
cs
|
| เขียนเมื่อ |
:
28 ส.ค. 54 17:52:07
A:125.24.44.200 X: TicketID:322284
|
|
|
|
อัตราส่วน R ต่อ r เป็นเท่าไหร่ครับ???
