ความคิดเห็นที่ 1 วาดรูปผิดป่าว?  วงใหญ่ต้องเป็นสีแดง  วงเล็กต้องเเป็นสีฟ้า จากคุณ : หัวโตนะ เขียนเมื่อ : 22 ก.ย. 54 20:48:57

ความคิดเห็นที่ 2 - - ผมบอกแล้วว่าให้ใช้สีอื่นๆ จะได้ไม่โดนลากเข้ารกเข้าพงอีก อย่างสีเขียวขอบฟ้าสลับดำตัดเหลืองอมชมพูขลิวม่วงเหลือบน้ำตาล อิอิ แก้ไขเมื่อ 22 ก.ย. 54 22:51:33 จากคุณ : ชโรนนท์ เขียนเมื่อ : 22 ก.ย. 54 22:47:34

ความคิดเห็นที่ 3 เมาคับ คิดถูกตอนแรกละ ดันมาคิดผิดอีกรอบ แล้วก็คิดถูกอีกรอบ งงตัวเองละ เช็กด้วยนะคับ = = จากคุณ : ชโรนนท์ เขียนเมื่อ : 22 ก.ย. 54 23:19:59

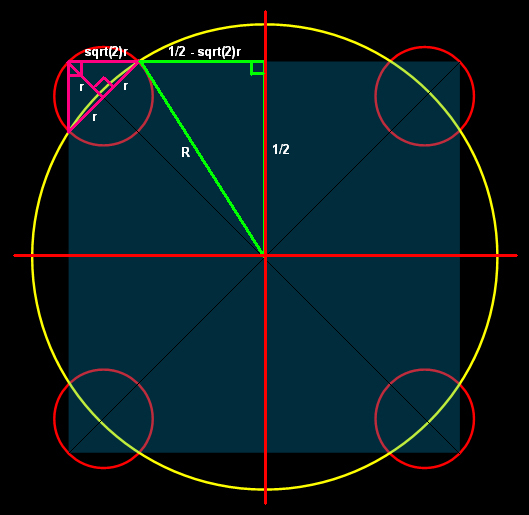
ความคิดเห็นที่ 4 วิธีของผมครับ คล้ายๆ ของ คุณ ชโรนนท์ จากรูป R2 = (1/2)2 + (1/2 - sqrt(2)r)2 = 2r2 - sqrt(2)r + 1/2 จะได้ว่า A + 4B = pR2 + 4pr2 = p(R2 + 4r2) = p(2r2 - sqrt(2)r + 1/2 + 4r2) = p(6r2 - sqrt(2)r + 1/2) พิจารณา สมการ y = 6r2 - sqrt(2)r + 1/2 ซึ่งเป็นสมการพาลาโบลาหงาย จะได้ว่า ค่าต่ำสุดของ y = 1/2 - (-sqrt(2))2/(4*6) = 5/12 เพราะฉะนั้น ค่าต่ำสุดของ A + 4B = p(5/12) = 5p/12 ตร.หน่วย เท่ากับคำตอบของ คุณ ชโรนนท์ ครับ ป.ล. กีบหมดครับ ขอติดไว้ก่อน แก้ไขเมื่อ 23 ก.ย. 54 10:40:52 จากคุณ : TIYHz เขียนเมื่อ : 23 ก.ย. 54 10:39:15

ความคิดเห็นที่ 5 กำหนด R = รัศมีของวงกลมเหลือง r = รัศมีวงกลมเล็ก A+4B = 4¶r2+ ¶(0.52)+¶(0.5-√2 r)2 d(A+4B )/dr = 8¶r+2¶(0.5-√2 r)(0-√2 ) = 0            = 8r + 4r -√2  = 0          r = √2/12 แทนค่า  4¶(√2/12)2+ ¶(0.52)+¶(0.5-√2 (√2/12)) 2 =5¶/12 จากคุณ : miryone (miryone) เขียนเมื่อ : 23 ก.ย. 54 12:40:22