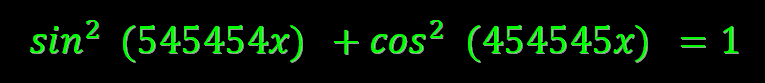 |
pi/999999
เนื่องจากขี้เกียจพิมพ์ กำหนดให้ A = 545454, B = 454545
sin2(Ax) + cos2(Bx) = 1
sin2(Ax) + 1 - sin2(Bx) = 1
sin2(Ax) - sin2(Bx) = 0
(sin(Ax)+sin(Bx)(sin(Ax)-sin(Bx)) = 0
จะได้ 2 กรณีคือ
1. sin(Ax) - sin(Bx) = 0
เปลี่ยนเป็นรูปผลคูณ 2 cos((A+B)x/2) sin((A-B)x/2) = 0
นั่นคือผลคูณนี้เป็นศูนย์ได้ก็ต่อเมื่อ
cos((A+B)x/2) = 0 หรือ sin((A-B)x/2) = 0
2. sin(Ax) + sin(Bx) = 0
เปลี่ยนเป็นรูปผลคูณ 2 sin((A+B)x/2) cos((A-B)x/2) = 0
นั่นคือผลคูณนี้เป็นศูนย์ได้ก็ต่อเมื่อ
sin((A+B)x/2) = 0 หรือ cos((A-B)x/2) = 0
ดังนั้น x ที่ทำให้สมการเป็นจริงจะสามารถหาได้จาก 4 กรณีดังนี้คือ
1) cos((A+B)x/2) = 0
(A+B)x/2 = (2n+1)pi/2 ; n = 1, 2,...
x = (2n-1)pi/(A+B)
2) cos((A-B)x/2) = 0
(A-B)x/2 = (2n-1)pi/2 ; n = 1, 2,...
x = (2n-1)pi/(A-B)
3) sin((A+B)x/2) = 0
(A+B)x/2 = n pi ; n = 1, 2,...
x = 2 n pi/(A+B)
4) sin((A-B)x/2) = 0
(A-B)x/2 = n pi ; n = 1, 2,...
x = 2 n pi/(A-B)
นั่นคือถ้านำทั้ง 4 กรณีข้างต้นมารวมกัน ก็จะได้คำตอบของสมการนี้คือ
x = n pi/(A+B) และ n pi/(A-B) เมื่อ n = 1, 2, 3,...
จะหาค่า x น้อยที่สุดเศษจะต้องน้อยที่สุดและส่วนจะต้องมากที่สุดดังนั้นเลือกใช้คำตอบ n pi/(A+B) และให้ n=1
จะได้ x = pi/999999 คือค่า x ที่เป็นจำนวนจริงบวกน้อยที่สุดที่ทำให้สมการ sin2(545454x) + cos2(454545x) = 1 เป็นจริง
ตอบ...pi/999999 หรือประมาณ 3.1416 x 10-6
แก้ไขเมื่อ 09 ต.ค. 54 01:25:54
แก้ไขเมื่อ 09 ต.ค. 54 01:25:11
แก้ไขเมื่อ 09 ต.ค. 54 01:23:46
แก้ไขเมื่อ 09 ต.ค. 54 01:21:47
แก้ไขเมื่อ 09 ต.ค. 54 01:21:09
แก้ไขเมื่อ 09 ต.ค. 54 01:20:15
| จากคุณ |
:
Seiki  
|
| เขียนเมื่อ |
:
9 ต.ค. 54 01:19:46
|
|
|
|
|
จำนวนจริงบวก x ที่เล็กที่สุด มีค่าเท่ากับเท่าไหร่ครับ???
