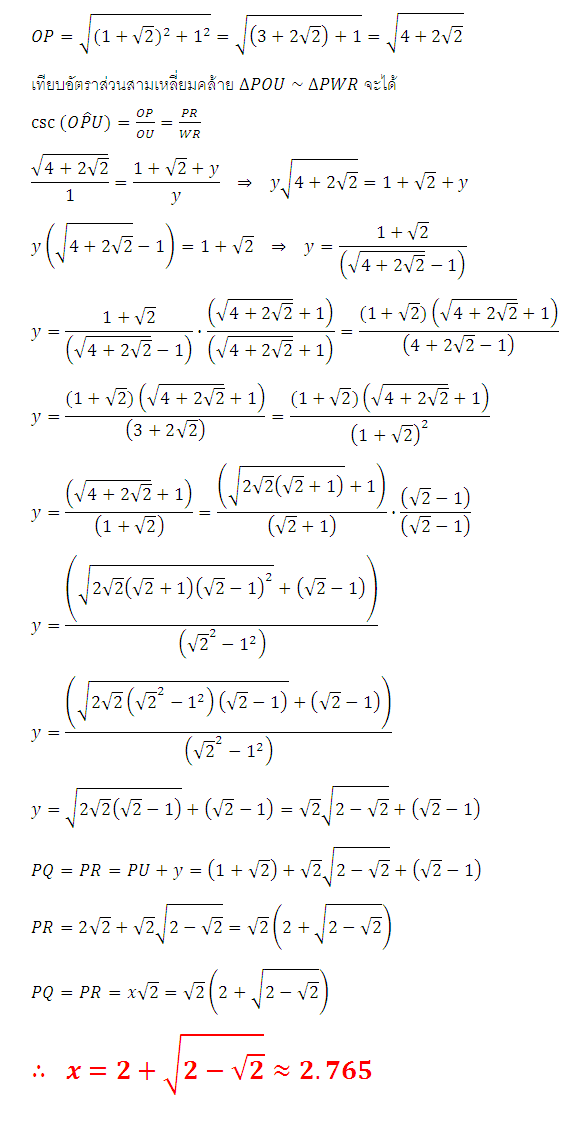|
*** ถ้าไม่ถูก ช่วยหาจุดผิดให้ผมด้วยนะครับ หมดแรงแล้วครับ ***
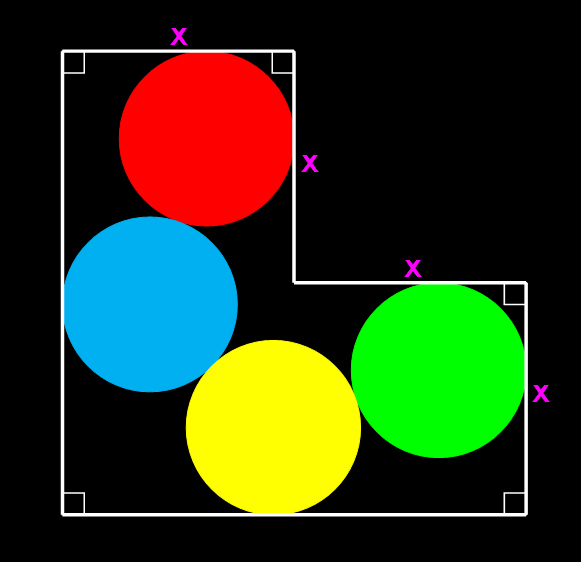
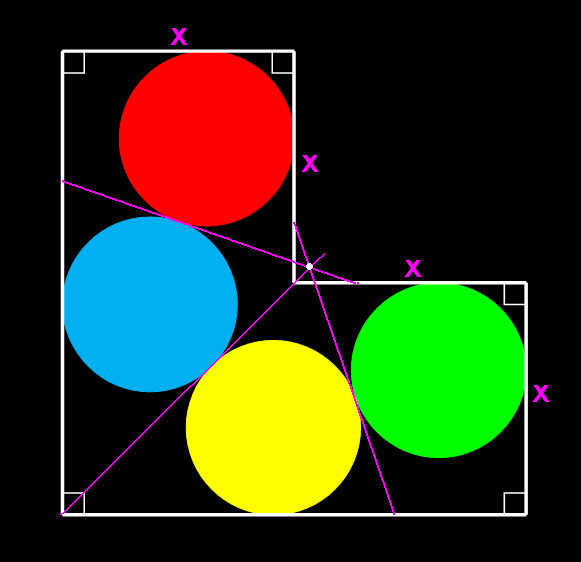
ขอเริ่มพิสูจน์จาก มุม B ในรูปเท่ากันหมดก่อนนะครับ
ลากเส้นจากจุด Q มาสัมผัสวงกลมทุกวง ซึ่งวงกลมแต่ละอันก็แตะกับวงกลมข้าง ๆ
ดังนั้น ความยาวเส้นจากจุด Q มายังจุดสัมผัสวงกลมแต่ละวงจะเท่ากันหมด
ดังนั้นเส้น QW = QT
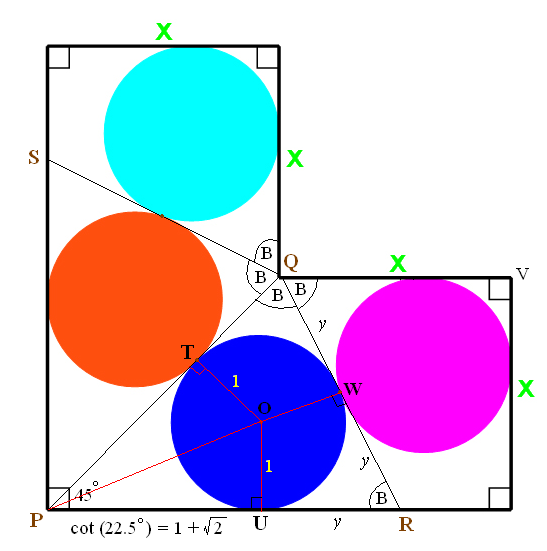
เพราะว่าลากจากจุดเดียวกัน มายังวงกลมรัศมีเท่ากัน ที่สัมผัสกัน มุมที่เกิดขึ้นจึงเท่ากันด้วย คือมุม B
ต่อไปพิสูจน์ว่า มุม PRQ = มุม B เพราะว่าเส้น QR ลากตัดเส้นขนาน ดังนั้นมุม VQR = มุม PRQ เพราะเป็นมุมแย้ง
สามเหลี่ยม PQR เป็นสามเหลี่ยมหน้าจั่วเพราะมีมุมที่ฐานเท่ากัน
ส่งผลให้ RW = RU = QW = QT ซึ่งสมมติให้เท่ากับ y
เส้นตรง PQ = sqrt(x2 + x2) = x รูท2
ดังนั้นเส้นตรง PO และเส้นตรง PW คือเส้นเดียวกัน ที่แบ่งครึ่งฐาน QR และแบ่งครึ่งมุม QPR ด้วย
เนื่องจาก POU เป็นสามเหลี่ยมมุมฉาก ทำให้ cot(OPU) = PU/OU = PU/1 = PU = cot(45o/2) = 1 + รูท2 โดยหาจากสูตรมุมครึ่ง tan(A/2) = รูท((1-cosA)/(1+cosA))
เชิญต่อที่ คห.ถัดไป
| จากคุณ |
:
basicguy 
|
| เขียนเมื่อ |
:
17 ต.ค. 54 20:44:42
|
|
|
|
ค่าของ x เท่ากับเท่าไหร่ครับ???
