 |
มาช่วยแก้ที่ผิดให้คุณ yariv_80 ครับ
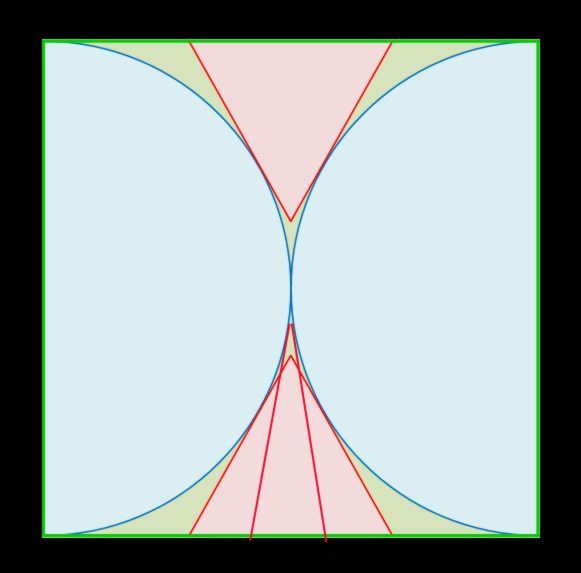
จากรูปใน คคห. 10
ความชันของ PQ = tan60o = sqrt(3)
วงกลมวงซ้าย กำหนดด้วยสมการ x2 + (y - 1)2 = 1 ---(*)
ต้องการหาพิกัดของ S ซึ่งเป็นจุดสัมผัสของวงกลมวงซ้ายกับ PQ
เพราะว่า ความชัน ณ จุดสัมผัส (S) = ความชันของ PQ = sqrt(3)
เพราะฉะนั้น สิ่งที่เราต้องการหา ก็คือ จุดบนวงกลมวงซ้ายที่มีความชัน ณ จุดนั้นเท่ากับ sqrt(3)
จากสมการ x2 + (y - 1)2 = 1
จะได้ว่า 2x + 2(y - 1)(dy/dx) = 0
แทน dy/dx = sqrt(3) จะได้ y = -x/sqrt(3) + 1 >>> นำไปแทนค่าในสมการ (*)
จะได้ x = sqrt(3)/2 และ y = 1/2 นั่นคือ พิกัดของจุด S คือ (sqrt(3)/2,1/2)
ต้องการหาพิกัดของ P ซึ่งเป็นจุดที่อยู่บนแกน X
สมมติให้พิกัดของจุด P คือ (a,0)
เพราะว่า จุด P(a,0) และ จุด S (sqrt(3)/2,1/2) อยู่บนเส้นตรงเดียวกัน (ความชัน = sqrt(3))
เพราะฉะนั้น (0 - 1/2)/(a - sqrt(3)/2) = sqrt(3) >>> a = 1/sqrt(3)
เพราะฉะนั้น พิกัดของจุด P คือ (1/sqrt(3),0)
โดยอาศัยความสมมาตรของรูป จะได้ว่า พิกัดของจุด R คือ (2 - 1/sqrt(3),0)
เพราะฉะนั้น |PR| = (2 - 1/sqrt(3)) - 1/sqrt(3) = 2(1 - 1/sqrt(3)) ป 0.8453 หน่วย ซึ่งก็คือสิ่งที่โจทย์ต้องการนั่นเอง
แก้ไขเมื่อ 20 ต.ค. 54 00:49:22
| จากคุณ |
:
TIYHz 
|
| เขียนเมื่อ |
:
20 ต.ค. 54 00:47:14
|
|
|
|
|
ความยาวในแต่ละด้านของสามเหลี่ยมสีชมพู เท่ากับเท่าไหร่ครับ???
