ความคิดเห็นที่ 1 x/y = 1.414 R/r = 2 จากคุณ : so-lar-ei เขียนเมื่อ : 12 พ.ย. 54 17:02:41

ความคิดเห็นที่ 2 อยากจะแสดงวิธีทำ แต่ใช้ iPad ตอบ ไม่สามารถจริงๆ(พิมพ์รูทยาก) รอท่านอื่นมาแสดงวิธีทำหละกันนะ จากคุณ : so-lar-ei เขียนเมื่อ : 12 พ.ย. 54 17:06:30

ความคิดเห็นที่ 3 R = 2r ดังนั้น R/r = 2 x = 2R+2r+2R = 4r+2r+4r = 10r y = 2R+r+R = 4r+r+2r = 7r ดังนั้น x/y = 10r/7r = 1.42857 แก้ไขเมื่อ 12 พ.ย. 54 18:52:12 จากคุณ : เมิร์ฟ (merf1970) เขียนเมื่อ : 12 พ.ย. 54 18:51:49

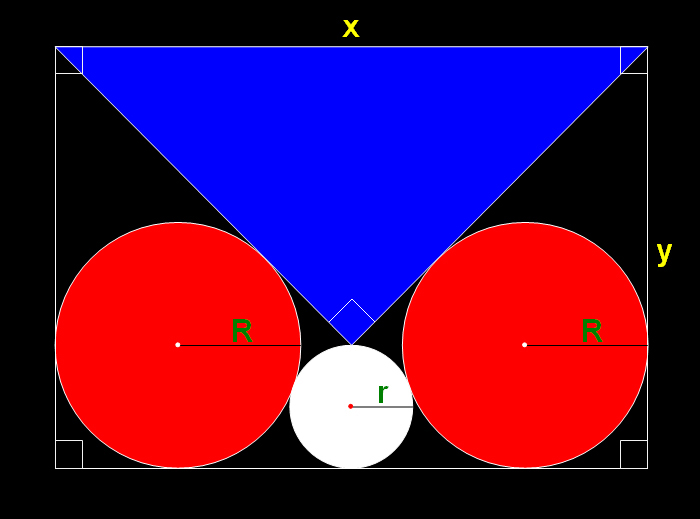
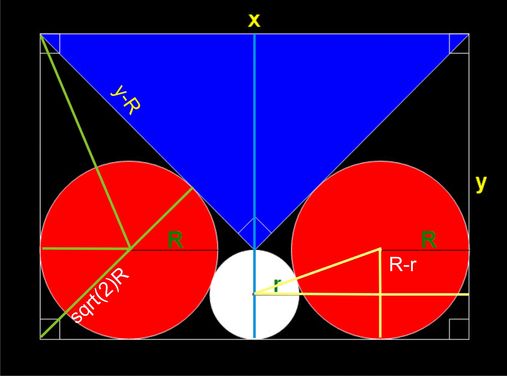
ความคิดเห็นที่ 4 ตั้งสมการ y = x/2 +2r --- (1) ,x/2 = xcos45sin45 สามเหลี่ยมทางซ้ายมือ y2 = (y-R)2 + (R+sqrt(2)R)2 y2 = y2-2yR+R2 +(1+sqrt(2))2R2 y             = (2+sqrt(2))R ---(2) สามเหลี่ยมสีเหลือง sqrt( (R+r)2 - (R-r)2 )= 2sqrt(Rr) x = 2R + 4sqrt(Rr) ---(3) แทน (2)และ(3)ใน(1) (2+sqrt(2))R = [2R + 4sqrt(Rr)]/ 2 + 2r (1+sqrt(2))R -2r = 2sqrt(Rr) ยกกำลัง2ทั้งสองข้างของสมการ (1+sqrt(2))2R2+4r2-4(1+sqrt(2))Rr = 4Rr (3+2sqrt(2))R2-(8+4sqrt(2))Rr+4r2 = 0 r2 หารสมการ (3+2sqrt(2))(R/r)2 - (8+4sqrt(2))R/r + 4 = 0 R/r = a (3+2sqrt(2))a2 - (8+4sqrt(2))a + 4 = 0 แก้สมการได้ a= 2,2/(3+2sqrt(2)) ***ตรงนี้สงสัยนิดหน่อยทำไมมีคำตอบ2ค่า ดูจากภาพ น่าเป็น 2 อย่างเดียว R = 2r หา x โดย แทน r = R/2 ใน (3) x = (2+2sqrt(2))R จาก(2) y = (2+sqrt(2))R x/y = sqrt(2) ความจริงลากเส้นตรงให้ผ่านจุดศูนย์กลางทั้งสองของวงกลมแดง แล้วตั้งสมมุติฐาน(ภาษาเลขเรียกว่าอะไรครับผมเรียกไม่ถูก) ว่าผ่านจุดยอดของสามเหลี่ยมมุมฉากสีน้ำเงินจะพิสูจน์ง่ายกว่านี้ คำตอบได้เท่ากัน แต่นั่นแหละ ไม่รู้จะอ้างว่าเส้นตรงผ่านจุดยอดได้อย่างไร จากคุณ : miryone เขียนเมื่อ : 12 พ.ย. 54 18:59:20

ความคิดเห็นที่ 5 โจทย์เดาเลขง่าย แต่พิสูจน์ยากคับ ผมว่าผมเคยเห็นใน Shortlist TMO ปีไหนซักปีเนี่ยแหละ คำตอบตามที่ตอบๆ เลยคับ แต่กำลังหาวิธีพิสูจน์สั้นๆ อยู่ รอแปบนะคับ จากคุณ : ชโรนนท์ เขียนเมื่อ : 12 พ.ย. 54 19:03:30

ความคิดเห็นที่ 6 ได้ละคับ เมานิดนึงตะกี้ เหอๆ จากคุณ : ชโรนนท์ เขียนเมื่อ : 12 พ.ย. 54 19:17:19

ความคิดเห็นที่ 7 ตอบ คุณ miryone เพราะว่า a = R/r ได้จากการแก้สมการที่ติด sqrt; (1+sqrt(2))R -2r = 2sqrt(Rr) เพราะฉะนั้น จึงต้องตรวจคำตอบ ซึ่งพบว่า a = 2/(3+2sqrt(2)) ทำให้ฝั่งซ้ายของสมการติดลบครับ เลยใช้ a ค่านั้นไม่ได้ ========== ส่วนการสมมติว่า เส้นตรงที่ลากผ่านจุดศูนย์กลางของวงกลมสีแดงทั้งสอง จะลากผ่านจุดยอดของสามเหลี่ยม แล้วคิดไปตามข้อสมมตินั้น คำตอบที่หาได้นั้นผมคิดว่ายังไม่เพียงพอที่จะสรุปว่า คำตอบนั้นเป็นคำตอบที่ถูกต้อง วิธีการนึงที่ทำได้ ก็คือ ใช้การพิสูจน์แบบ Contradiction ซึ่งทำได้โดยสมมติว่า เส้นตรงที่ลากผ่านจุดศูนย์กลางของวงกลมสีแดงทั้งสอง จะ "ไม่" ลากผ่านจุดยอดของสามเหลี่ยม แล้วแยกคิด 2 กรณี ได้แก่ 1. จุดยอดของสามเหลี่ยมอยู่เหนือเส้นตรงเส้นนั้น กับ 2. จุดยอดของสามเหลี่ยมอยู่ใต้เส้นตรงเส้นนั้น ถ้าเกิดว่าทั้ง 2 กรณีมีข้อขัดแย้งอะไรซักอย่างเกิดขึ้น เราจึงสรุปว่า เส้นตรงเส้นนั้นต้องลากผ่านจุดยอดของสามเหลี่ยม แล้วก็คิดหาคำตอบปกติครับ ป.ล. ดูเหมือนจะยุ่งยากกว่าเดิมอีกแน่ะ แก้ไขเมื่อ 12 พ.ย. 54 22:46:13 จากคุณ : TIYHz เขียนเมื่อ : 12 พ.ย. 54 22:22:32

ความคิดเห็นที่ 8 ถาม คุณ ชโรนนท์ ครับ ว่า ทำไมถึงรู้ว่า CE ตั้งฉากกับ BG ครับ จากคุณ : TIYHz เขียนเมื่อ : 12 พ.ย. 54 22:30:15

ความคิดเห็นที่ 9 โอ๊ะ ตายๆ จริงด้วยแฮะ - -" ท่าทางคงต้องคำนวณตรีโกณนิดๆ ละคับ ใช้เรขาอย่างเดียวคงยาวแน่ จากคุณ : ชโรนนท์ เขียนเมื่อ : 12 พ.ย. 54 23:00:50