|
ใช้แนวคิดของ คุณ ชโรนนท์ ครับ
จาก (sqrt(2+sqrt(2+sqrt(2+x)))+sqrt(3)sqrt(2-sqrt(2+sqrt(2+x))) = 2x
แทน x = 2cos(8A)
จะได้ (sqrt(2+sqrt(2+sqrt(2+2cos(8A))))+sqrt(3)sqrt(2-sqrt(2+sqrt(2+2cos(8A)))) = 4cos(8A)
2cos(A) + 2sqrt(3)sin(A)= 4cos(8A)
(1/2)cos(A) + (sqrt(3)/2)sin(A) = cos(8A)
cos(pi/3)cos(A) + sin(pi/3)sin(A) = cos(8A)
cos(pi/3 - A) = cos(8A)
คิดมุมเล็กๆ ได้ว่า pi/3 - A = 8A หรือ pi/3 - A = -8A
เพราะฉะนั้น A = pi/27 หรือ A = -pi/21
เพราะฉะนั้น x = 2cos(8pi/27) หรือ 2cos(-8pi/21)
เมื่อตรวจคำตอบแล้ว พบว่าใช้ x = 2cos(8pi/27) ได้ค่าเดียว ###
แก้ไขเมื่อ 18 พ.ย. 54 16:08:21
แก้ไขเมื่อ 18 พ.ย. 54 16:01:35
| จากคุณ |
:
TIYHz 
|
| เขียนเมื่อ |
:
18 พ.ย. 54 15:40:48
|
|
|
|

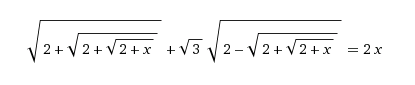

 จะไปสมมติ x ทำไม ?
จะไปสมมติ x ทำไม ? 
