ความคิดเห็นที่ 1 เห็นชื่อกระทู้แว้บแรกแล้วตกใจ เป็นเกียรติอย่างยิ่งครับ การพิสูจน์สูตรที่ 2 ให้ P(n) แทนข้อความ F(2n) = (2F(n - 1) + F(n))F(n) ทุกจำนวนเต็ม n ณ 0 เพราะว่า F(2) = (2F(0) + F(1))(F(1)) = (2 x 0 + 1)(1) = 1 เพราะฉะนั้น P(1) เป็นจริง สมมติ P(k) เป็นจริง ทุกจำนวนเต็ม 1 ฃ k ฃ n              F(2k) = (2F(k - 1) + F(k))F(k)              F(2k) + F(2k - 1) = (2F(k - 1) + F(k))F(k) + F(2k - 1)              F(2k + 1) = (2F(k - 1) + F(k))F(k) + F(2k - 1)              F(2k + 1) + F(2k) = (2F(k - 1) + F(k))F(k) + F(2k - 1) + F(2k)              F(2k + 2) = (2F(k - 1) + F(k))F(k) + [F(2k) - F(2k - 2)] + F(2k)              F(2(k + 1)) = (2F(k - 1) + F(k))F(k) + 2F(2k) - F(2(k - 1))              F(2(k + 1)) = (2F(k - 1) + F(k))F(k) + 2((2F(k - 1) + F(k))F(k)) - (2F(k - 2) + F(k - 1))F(k - 1)              F(2(k + 1)) = 3(2F(k - 1) + F(k))F(k) - (2F(k - 2) + F(k - 1))F(k - 1)              F(2(k + 1)) = 3(F(k - 1) + F(k + 1))F(k) - (2F(k) - F(k - 1))F(k - 1)              F(2(k + 1)) = 3F(k - 1)F(k) + 3F(k + 1)F(k) - 2F(k)F(k - 1) + F(k - 1)F(k - 1)              F(2(k + 1)) = F(k - 1)F(k) + 3F(k + 1)F(k) + F(k - 1)F(k - 1)              F(2(k + 1)) = F(k - 1)F(k) + 3F(k + 1)F(k) + (F(k + 1) - F(k))F(k - 1)              F(2(k + 1)) = F(k - 1)F(k) + 3F(k + 1)F(k) + F(k + 1)F(k - 1) - F(k)F(k - 1)              F(2(k + 1)) = 3F(k + 1)F(k) + F(k + 1)F(k - 1)              F(2(k + 1)) = 3(F(k) + F(k - 1))F(k) + F(k + 1)F(k - 1)                  F(2(k + 1)) = 3F(k)F(k) + 3F(k - 1)F(k) + F(k + 1)F(k - 1)                  F(2(k + 1)) = 2F(k)F(k) + 2F(k)F(k - 1) + F(k + 1)F(k - 1) + F(k)F(k) + F(k)F(k - 1)              F(2(k + 1)) = 2F(k)F(k) + 2F(k)F(k - 1) + F(k + 1)F(k - 1) + F(k)(F(k) + F(k - 1))              F(2(k + 1)) = 2F(k)F(k) + 2F(k)F(k - 1) + F(k + 1)F(k) + F(k + 1)F(k - 1)              F(2(k + 1)) = (2F(k) + F(k + 1))(F(k) + F(k - 1))              F(2(k + 1)) = (2F(k) + F(k + 1))F(k + 1) เพราะฉะนั้น P(k + 1) เป็นจริง เพราะฉะนั้น สูตร F(2n) = (2F(n - 1) + F(n))F(n) ทุกจำนวนเต็ม n ณ 0 เป็นจริง ### ป.ล. ขออภัยถ้าไม่กระชับ เพราะคิดไปพิมพ์ไปครับ ป.ล.2 เข้าใจว่า คุณ บัตรผ่าน ต้องการให้พิสูจน์ยังไง แต่ผมยังคิดไม่ออก เลยทำวิธีนี้ให้ดูก่อนครับ ^^ แก้ไขเมื่อ 22 พ.ย. 54 01:13:56 แก้ไขเมื่อ 22 พ.ย. 54 01:11:20 จากคุณ : TIYHz เขียนเมื่อ : 22 พ.ย. 54 01:04:46

ความคิดเห็นที่ 2 ไม่เชิญเรา งอนละ จากคุณ : mint_la เขียนเมื่อ : 22 พ.ย. 54 01:06:18

ความคิดเห็นที่ 3 เชิญคุณ mint_la ด้วยครับ ให้เวลาถึง วันเสาร์ จะมาเฉลยนะครับ ^_^ จากคุณ : บัตรผ่านอัจฉริยะ เขียนเมื่อ : 22 พ.ย. 54 01:16:05 A:125.24.36.116 X: TicketID:327013

ความคิดเห็นที่ 4 คุณ TIYHz ถึกมาก คาระวะสามจอก m(_ _)m ตะกี้แอบงงเรื่อง T(n) = log(n) ครับ T(n) = k*T(n/2^k)+k*O(1) หรือเปล่าครับ แก้ไขเมื่อ 22 พ.ย. 54 01:57:00 แก้ไขเมื่อ 22 พ.ย. 54 01:27:10 จากคุณ : bakasama เขียนเมื่อ : 22 พ.ย. 54 01:21:21

ความคิดเห็นที่ 5 เก่งนะครับ (แต่อยากรู้จัง..... ใครที่ถอดล็อกอินเพื่อเรียกตัวเองว่าอัจฉริยะ) จากคุณ : นกแคปหมู เขียนเมื่อ : 22 พ.ย. 54 01:49:54

ความคิดเห็นที่ 6 ข้อ 1 F(2n-1) = F(n-1)^2 + F(n)^2 จาก Phi^n = F(n)Phi + F(n-1)-----------------(0) Phi^2 = F(2)Phi+F(1) Phi^2 = Phi+1---------------------------------(1) พิสูจน์สมการ F(m+n-1) = F(m)F(n)  +  F(m-1)F(n-1)  ? ให้ F(m+n-1) = F(m)F(n)  +  F(m-1)F(n-1) ดังนั้น F(m+n) = F(m)F(n+1)  +  F(m-1)F(n)-------------------------(2) จาก Phi^(m+n) = Phi^m x Phi^n แทน(0) ลงในสมการ F(m+n)Phi + F(m+n-1)     =       [F(m)Phi + F(m-1)]  x  [F(n)Phi + F(n-1)]                                       =       F(m)F(n)Phi^2   +   F(m)F(n-1)Phi  +  F(m-1)F(n)Phi  +  F(m-1)F(n-1) แทน(1) ลงในสมการ F(m+n)Phi + F(m+n-1)     =       F(m)F(n)(Phi + 1)   +   F(m)F(n-1)Phi  +  F(m-1)F(n)Phi  +  F(m-1)F(n-1)                                        =      [   F(m)F(n) + F(m)F(n-1) + F(m-1)F(n)  ] Phi  +   F(m)F(n)  +  F(m-1)F(n-1)                                        =      [   F(m)F(n+1) + F(m-1)F(n)  ] Phi  +   F(m)F(n)  +  F(m-1)F(n-1) แทน(2) ลงในสมการ F(m+n)Phi + F(m+n-1)     =       F(m+n)Phi  +  F(m)F(n)  +  F(m-1)F(n-1) ดังนั้น   F(m+n-1)                        = F(m)F(n)  +  F(m-1)F(n-1) แทน m = n จะได้ว่า                              F(2n-1) = F(n-1)^2 + F(n)^2          เป็นจริง จากคุณ : ตื่นมาคิด (mint_la) เขียนเมื่อ : 22 พ.ย. 54 04:49:31

ความคิดเห็นที่ 7 เขาเชิญคนที่สนใจ #3 คุณ mint_la บอก เขาไม่เชิญคุณ mint_la แสดงว่าคุณ mint_la ไม่ใช่ คนที่สนใจ ถ้าคุณ mint_la ไม่สนใจ แล้วทำไมงอนครับ จากคุณ : ผลึกความคิด เขียนเมื่อ : 22 พ.ย. 54 08:32:40

ความคิดเห็นที่ 8 O() ไม่ใช่ logn จากคุณ : BLiNDiNG เขียนเมื่อ : 22 พ.ย. 54 10:05:55

ความคิดเห็นที่ 9 คุณ BLiNDiNG ขยายความหน่อยได้ไหมครับ ทำไมไม่ใช่ logn จากคุณ : บัตรผ่านอัจฉริยะ เขียนเมื่อ : 22 พ.ย. 54 10:15:38 A:125.24.40.91 X: TicketID:327013

ความคิดเห็นที่ 10 เก่งกันจัง    เด็กแว้นงงเลย จากคุณ : precham เขียนเมื่อ : 22 พ.ย. 54 10:51:11

ความคิดเห็นที่ 11 ลองจำลองการทำงาน ใช้สูตรนี้ ในการคำนวณ ดูว่า จะหา  F(341) ต้องหา F(?) ของอะไรบ้าง       341     170 171    84  85  86    41  42  43    20  21  22     9  10  11     4   5   6     1   2   3         1   2             1 ดูแล้ว ถ้าไม่ทำงานซ้ำซ้อนกัน ปริมาณงานน่าจะ O(log(n)) ได้ ถ้าเรียกตัวเองตามสูตรตรงๆ แล้วปล่อยให้มันทำงานซ้ำซ้อนกัน จะเกิน O(log(n)) จากคุณ : ผลึกความคิด เขียนเมื่อ : 22 พ.ย. 54 10:59:32

ความคิดเห็นที่ 12 #11 งานซ้ำซ้อนแก้โดยใช้ Dynamic Programming ผมดูแล้วอัตราการเรียก F(n) ซ้ำ เกิดมากสุด 1 ครั้งต่อการแตก n-> n/2 เพราะที่เหลือจะซ้ำกัน คิดเป็น O(log(n)) แก้ไขเมื่อ 22 พ.ย. 54 11:56:09 แก้ไขเมื่อ 22 พ.ย. 54 11:52:55 จากคุณ : bakasama เขียนเมื่อ : 22 พ.ย. 54 11:49:19

ความคิดเห็นที่ 13 เก่งมากเลยครับ ทั้งคุณ TIYHz และคุณ mint_la ยังมีการพิสูจน์ โดยเริ่มจาก สมการรูปแบบพื้นฐานของ Fibonacci นะครับ คือตอนทำ ผมก็ไม่รู้หรอก ว่าจะเปลี่ยนรูปออกมาแบบนี้ได้ จากคุณ : บัตรผ่านอัจฉริยะ เขียนเมื่อ : 22 พ.ย. 54 12:14:04 A:125.24.40.91 X: TicketID:327013

ความคิดเห็นที่ 14 ช่วยอีกแรงครับ จะพิสูจน์ว่า F2n-1 = Fn2 + Fn-12 เมื่อ 0 ฃ k < n จะได้ว่า Fn+kFn-k  +  Fn+k-1Fn-k-1  =  Fn+k(Fn-k-1 + Fn-k-2)  +  Fn+k-1Fn-k-1                                         =  Fn+kFn-k-1  +  Fn+kFn-k-2  +  Fn+k-1Fn-k-1                                         =  (Fn+kFn-k-1  +  Fn+k-1Fn-k-1)  +  Fn+kFn-k-2                                         =  Fn-k-1(Fn+k  +  Fn+k-1)  +  Fn+kFn-k-2                                         =  Fn+k+1Fn-k-1  +  Fn+kFn-k-2 ดังนั้น  Fn+kFn-k  +  Fn+k-1Fn-k-1  =  Fn+k+1Fn-k-1 + Fn+kFn-k-2 _____(1) อาศัยสมการที่(1)จะได้ว่า     Fn2 + Fn-12   =   FnFn + Fn-1Fn-1                         =   Fn+1Fn-1 + FnFn-2                         =   Fn+2Fn-2 + Fn+1Fn-3                            ......                            ......                            ......                         =   Fn+(n-1)F1  +   Fn+(n-2)F0                         =   F2n-1F1 + F2n-2F0                                                   =  F2n-1                               ;  F0 = 0 , F1 = 1 ดังนั้น  F2n-1 = Fn2 + Fn-12       ## จากคุณ : อิอิคุง เขียนเมื่อ : 22 พ.ย. 54 12:25:57

ความคิดเห็นที่ 15 ตามที่ #11 #12 บอกครับ ถ้าไม่ใช้ dynamic ให้เก็บส่วนที่ได้ทำไปแล้ว ก็จะซ้ำซ้อนกันเกินกว่า log n จากคุณ : BLiNDiNG เขียนเมื่อ : 22 พ.ย. 54 12:34:15

ความคิดเห็นที่ 16 ต่อไปพิสูจน์ว่า  F2n  =  (Fn  +  2Fn-1)Fn โดยอาศัยสูตร F2n-1 จาก           F2n-1  =  F2n-2  +  F2n-3 จะได้   Fn2  +  Fn-12  =  F2n-2  +  Fn-12  +  Fn-22                        F2n-2  =  Fn2  -  Fn-22                        F2n-2  =  (Fn-1  +  Fn-2)2  -  Fn-22                        F2n-2  =  Fn-12  +  2Fn-1Fn-2                     F2(n-1)   =  (Fn-1  +  2Fn-2)Fn-1 แทนค่า n ด้วย n+1     F2n  =  (Fn  +  2Fn-1)Fn   ## จากคุณ : อิอิคุง เขียนเมื่อ : 22 พ.ย. 54 13:08:41

ความคิดเห็นที่ 17 ด้วยความสามารถที่มีอันจำกัด F(2n-1) = F(n-1)^2 + F(n)^2 F(2n) = ( 2 F(n-1) + F(n) ) F(n) F(2n+1) = F(2n)+F(2n-1) =F(n-1)^2 + F(n)^2 + 2 F(n-1)F(n) + F(n) ^2 =(F(n-1)+F(n))^2 + F(n) ^2 =(F(n+1)^2 + F(n) ^2) ดังนั้น ถ้า พิสูจน์ ข้อ2ได้ ก่อน ก็ใช้อุปนัย มาช่วยพิสูจน์ข้อ1ได้ กลับกัน ถ้าพิสูจน์ข้อ1ได้ก่อน ข้อ2 ก็พิสูจน ตามที่ผมเขียนได้ ตอบอย่างนี้ จะได้คะแนนถึงครึ่งมั้ยนี่ จากคุณ : aLITTLEspaceAround7day เขียนเมื่อ : 22 พ.ย. 54 17:11:20

ความคิดเห็นที่ 18 นี่สินะคือโลกของ คณิตศาสตร์  นักเคมีอย่างผมคงไม่รู้เรื่อง  - -" จากคุณ : Organic_D เขียนเมื่อ : 22 พ.ย. 54 20:01:01

ความคิดเห็นที่ 19 พิสูจน์ได้แค่นี้ครับ ที่เหลือตาม คุณ อิอิคุง ครับ จากรูป (ไม่ต้องสนใจเส้นสีชมพู) จะได้ว่า (F(n))2 + (F(n - 1))2 = F(n)(F(n) + F(n - 1)) - F(n - 1)(F(n) - F(n - 1)) = (F(n - 1) + F(n - 2))F(n + 1) - F(n - 1)F(n - 2) = F(n - 1)F(n + 1) + (F(n + 1) - F(n - 1))F(n - 2) = F(n - 1)F(n + 1) + F(n)F(n - 2) ... เหมือนสมการนึงใน คคห. 14 ครับ จากคุณ : TIYHz เขียนเมื่อ : 22 พ.ย. 54 23:06:13

ความคิดเห็นที่ 20 ถ้า ขี้เกียจรอ ถึงวันเสาร์ ... ขอเพียง คุณ TIYHz บอกมาคำเดียว ผมจะเฉลยเลยครับ จากคุณ : บัตรผ่านอัจฉริยะ เขียนเมื่อ : 22 พ.ย. 54 23:24:56 A:125.24.40.91 X: TicketID:327013

ความคิดเห็นที่ 21 เห็น คห 19 ยอมรับว่าขนลุกคับ สวยมาก... จากคุณ : ชโรนนท์ เขียนเมื่อ : 22 พ.ย. 54 23:29:16

ความคิดเห็นที่ 22 คุณ บัตรผ่าน พอใจกับวิธีของผม (คคห. 19) หรือเปล่าครับ ผมตั้งสมการจากรูปสุดฮิตเลยนะนั่น อิอิ จากคุณ : TIYHz เขียนเมื่อ : 22 พ.ย. 54 23:33:58

ความคิดเห็นที่ 23 คุณ ชโรนนท์... อะไรสวยมากครับ รูปหรือวิธีคิดครับ (ถ้าเป็นอย่างหลังจะดีใจมาก แต่ยังไงก็ขอบคุณที่ชมครับ ^^) จากคุณ : TIYHz เขียนเมื่อ : 22 พ.ย. 54 23:37:31

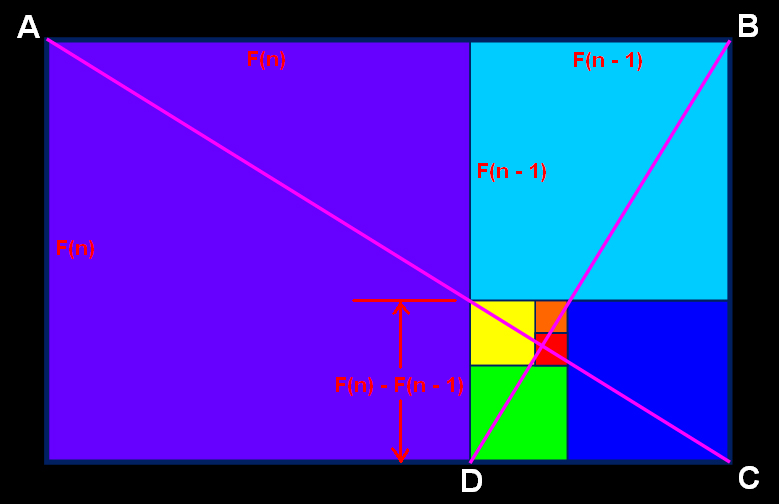
ความคิดเห็นที่ 24 ชอบมาเลยครับ TIYHz ผมขอเฉลยวิธีคิดของผมเลยแล้วกันนะครับ เนื่องจากตอบกันมามากพอสมควรแล้ว F(n) = 0 ; เมื่อ n=0 F(n) = 1 ; เมื่อ n=1 F(n) = F(n-1) + F(n-2) ..... (1) สมมติให้ n มีค่ามากๆ แล้วลองคำนวณไปเรื่อยๆ F(n) = (F(n-2) + F(n-3)) + F(n-2) F(n) = 2F(n-2) + F(n-3) ...... (2) F(n) = (2F(n-3)+2F(n-4)) + F(n-3) F(n) = 3F(n-3) + 2F(n-4) ...... (3) F(n) = (3F(n-4)+3F(n-5)) + 2F(n-4) F(n) = 5F(n-4) + 3F(n-5) ...... (4) F(n) = (5F(n-5)+5F(n-6)) + 3F(n-5) F(n) = 8F(n-5) + 5F(n-6) ...... (5) F(n) = (8F(n-6)+8F(n-7)) + 5F(n-6) F(n) = 13F(n-6) + 8F(n-7) ...... (6) พิจารณา (1),(2),(3),(4),(5),(6) สัมประสิทธิ์ หน้า พจที่ 1 และ พจน์ที่ 2 ของแต่ละสมการ เป็นลำดับ Fibonucci พจที่ 1 => 1 , 2 , 3 , 5 , 8 , 13 ... พจที่ 2 => 1 , 1 , 2 , 3 , 5 , 8 ... เนื่องจาก ตัวคูณ หน้าพจน์ที่ 1 ของสมการ (i) เกิดจาก ผลรวมของ ตัวคูณ ของ พจน์ที่ 1 และ 2 ของสมการ (i-1) และตัวคูณ หน้าพจน์ที่ 2 ของสมการ (i) ก็เท่ากับ ตัวคูณ ของ พจน์ที่ 1 ของสมการ (i-1) เที่ยบค่าคงที่ของ สัมประสิทธิ์ กับอนุกรม Fibonucci และจัดรูปใหม่ จะได้สมการ F(n) = F(m)F(n-(m-1)) + F(m-1)F(n-m) จัดรูปใหม่ได้เป็น F(n) = F(m)F(n-m+1) + F(m-1)F(n-m) โดยที่ 1<m<n และเป็นจำนวนเต็ม ถึงจุดนี้ ผมเลือก m ที่สัมพันธ์กับ n โดยให้ m=(n+1)/2 เมื่อ n เป็นเลขคี่ และ m=n/2 เมื่อ n เป็นเลขคู่ กรณีที่ 1 เมื่อ n เป็นเลขคี่ m=(n+1)/2 n=2m-1 F(n) = F(m)F(n-m+1) + F(m-1)F(n-m) F(2m-1) = F(m)F(2m-1-m+1) + F(m-1)F(2m-1-m) F(2m-1) = F(m)F(m) + F(m-1)F(m-1) F(2m-1) = F(m)^2 + F(m-1)^2 .... เปลี่ยน m เป็น n ก็จะได้สูตรที่ 1 กรณีที่ 2 เมื่อ n เป็นเลขคู่ m=n/2 F(n) = F(m)F(n-m+1) + F(m-1)F(n-m) F(2m) = F(m)F(2m-m+1) + F(m-1)F(2m-m) F(2m) = F(m)F(m+1)) + F(m-1)F(m) F(2m) = (F(m+1) + F(m-1))F(m) F(2m) = (F(m)+ F(m-1)+ F(m-1))F(m) F(2m) = (2F(m-1)+ F(m))F(m) .... เปลี่ยน m เป็น n ก็จะได้สูตรที่ 2 จากคุณ : บัตรผ่านอัจฉริยะ เขียนเมื่อ : 23 พ.ย. 54 00:27:38 A:125.24.40.91 X: TicketID:327013

ความคิดเห็นที่ 25 #24 จำได้ละสูตรนี้.. เหมือนตอนอยู่มัธยมผมก็ใช้วิธีนี้หล่ะครับ ลองแตกพจน์แล้วได้ Fib คูณกัน จากคุณ : bakasama เขียนเมื่อ : 23 พ.ย. 54 13:58:11

ความคิดเห็นที่ 26 นั่งนึกว่าอันแรกเคยเจอที่ไหน . . . เคย proof ในโจทย์ของเว็บๆหนึ่ง F(n-1) F(n) F(n+1) F(n+2) F(n+3) F(n+4) F(2n-1) F(n-1) 1 0 1 1 2 จากคุณ : PattaraS เขียนเมื่อ : 23 พ.ย. 54 20:38:27 A:115.87.133.132 X: TicketID:251123

ความคิดเห็นที่ 27 นั่งนึกว่าอันแรกเคยเจอที่ไหน . . . เคย proof ในโจทย์ของเว็บๆหนึ่ง วิธีคิด ให้ F(m) = aF(n) + bF(n-1) เมื่อ m>=n จะพบว่า a,bเป็นลำดับ fibonacci F(n-1) = 0F(n) + 1F(n-1) F(n) = 1F(n) + 0F(n-1) F(n+1) = 1F(n) + 1F(n-1) F(n+2) = 2F(n) + 1F(n-1) F(n+3) = 3F(n) + 2F(n-1) . . . F(2n-1) = F(n)F(n) + F(n-1)F(n-1) ป.ล. ผมกดpreview มันก็ส่งข้อความซะงั้น - - พันทิพย์มีปัญหากับChromeรึเปล่าครับ จากคุณ : PattaraS เขียนเมื่อ : 23 พ.ย. 54 20:42:40 A:115.87.133.132 X: TicketID:251123

ความคิดเห็นที่ 28 อยากถามคุณ จขกท. ว่าวิธีการแก้หา fibonacci แบบคุณ จขกท. ดีกว่าวิธีอื่นที่ได้ O(lgn) อย่างไรครับ? (วิธีอื่นคือ recurrence ที่แก้แล้วกับตั้งคูณเมตริกซ์ยกกำลังซึ่งสามารถหาได้ใน O(lgn) เช่นเดียวกัน) จากคุณ : PattaraS เขียนเมื่อ : 23 พ.ย. 54 21:12:30 A:115.87.133.132 X: TicketID:251123

ความคิดเห็นที่ 29 จริงๆแล้ว วิธีหา fibonucci วิธีนี้ ยังไม่ใช่วิธีที่ดีที่สุดครับ มีสูตรที่หาค่า fibonucci ได้ในสมการเดียว โดยใช้สัดส่วนทองคำ (golden ratio) ถ้าใช้วิธีนั้น จะเป็น O(1) ได้เลย สูตรมันเครื่องหมายเยอะ ผมพิมพ์ไม่ถนัด ลองหาในวิกิเอาแล้วกันครับ ส่วนวิธี recurrence ที่แก้แล้วกับตั้งคูณเมตริกซ์ยกกำลัง ผมเองก็ไม่เคยทราบมาก่อน จึงไม่รู้ว่าแบบไหนดีกว่าเหมือนกัน จากคุณ : บัตรผ่านอัจฉริยะ เขียนเมื่อ : 23 พ.ย. 54 22:31:37 A:125.24.44.50 X: TicketID:327013

ความคิดเห็นที่ 30 สูตรที่เป็น golden ratio ผมเข้าใจว่าเป็นสูตรเดียวกับที่ได้จากการแก้ recurrence relation นะครับ อย่างไรก็ตาม ผมเข้าใจว่า เราจะต้องหา (golden ratio)ยกกำลัง n เพื่อหา F(n) ซึ่งการหาเลขยกกำลังทำได้ใน O(lgn) โดยใช้ Algorithm แบบ Divide&Conquer ผมเลยยังมองไม่เห็นว่าจะหา O(1) จากไหน ซึ่งถ้าผมเข้าใจผิดก็ช่วยชี้แจงด้วยนะครับ ส่วนวิธีตั้งเมตริกซ์ ก็ทำดังนี้ครับ ถ้าเราเอาเมตริกซ์ขนาด 2x2 ซึ่งประกอบด้วย [0,1:1,1] มาคูณกับ vector [F(n):F(n+1)] จะได้ผลลัพธ์เป็น [F(n+1),F(n+2)] ดังนั้นถ้าเราเอา [0,1:1,1]^n คูณกับ [F(0):F(1)] ก็จะได้ผลลัพธ์เป็น [F(n):F(n+1)] ครับซึ่งการหา [0,1:1,1]^n ก็ทำได้ใน O(lgn) โดยใช้ Algorithm แบบ Divide&Conquer เช่นเดียวกันครับ จากคุณ : PattaraS เขียนเมื่อ : 23 พ.ย. 54 23:00:26 A:115.87.133.132 X: TicketID:251123

ความคิดเห็นที่ 31 ถ่ายรูปกระดาษทดมาฝาก คุณ บัตรผ่าน (พอดีว่าวันนี้ใข้กล้อง อิอิ) ที่จริงผมก็มาถูกทางแล้วนะ แต่ดันละความพยายามไปก่อน เพราะคิดว่ามันคงไปต่อไม่ได้ T T จากคุณ : TIYHz เขียนเมื่อ : 24 พ.ย. 54 10:50:08