ตอบ sqrt(24)
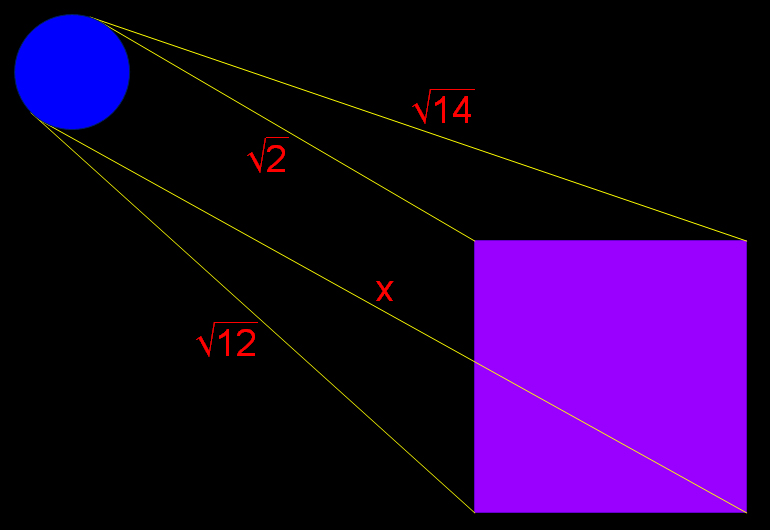
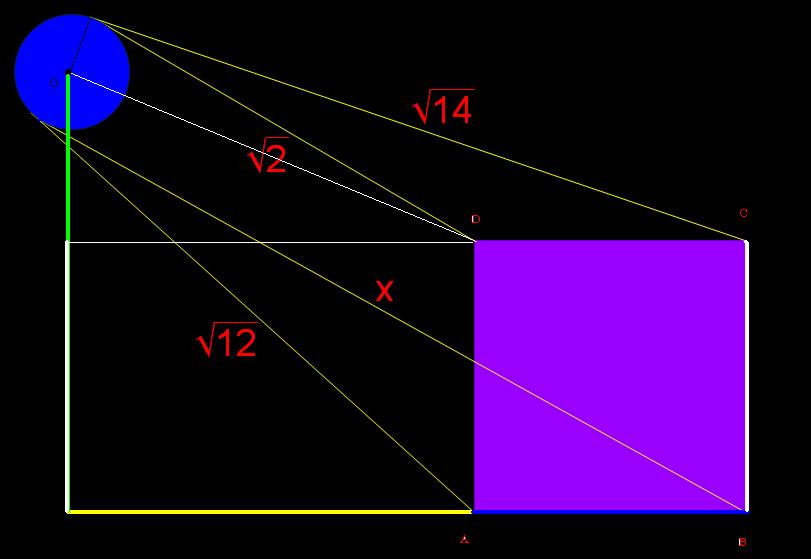
ให้จุดของสี่เหลี่ยม ที่ต่อกับเส้น sqrt(2) คือ A, ต่อกับเส้น sqrt(14) คือ B, ต่อกับเส้น x คือ C, ต่อกับเส้น sqrt(12) คือ D
ให้จุดศูนย์กลางของวงกลม คือ O และรัศมี = r
จากจุด O ลากเส้นตั้งฉากกับส่วนต่อของ BA ที่จุด P และส่วนต่อของ CD ที่จุด Q ดังนั้น PA = QD, PB = QC
จาก Pythagorus จะได้
OA^2 = 2+r^2; OB^2 = 14+r^2; OC^2 = x^2+r^2; OD^2 = 12+r^2
แต่ OB^2 = OP^2 + PB^2; OA^2 = OP^2 + PA^2
และ OC^2 = OQ^2 + QC^2; OD^2 = OQ^2 + QD^2
แต่ PA = QD, PB = QC
ดังนั้น OB^2-OA^2 = OC^2-OD^2
แทนค่าจะได้: 14+r^2 - (2+r^2) = x^2+r^2- (12+r^2)
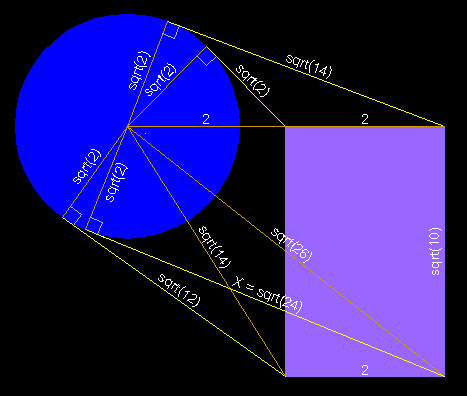
----> x^2 = 24
x = sqrt(24)
ค่าของ x เท่ากับเท่าไหร่ครับ??? [ส่งท้ายปี 2554]
