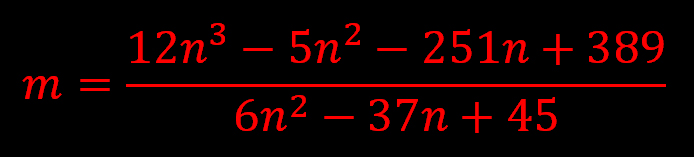n = 14
วิธีคิด
หารยาว จะเหลือเศษ 3n^2 +66n -106
แต่ 6n^2 - 37n + 45 = (2n-9)(3n-5)
จากทฤษฎีเศษเหลือ 3n^2 +66n -106 หารด้วย 2n-9 จะเหลือเศษ 1007/4
แต่ n เป็นจำนวนเต็ม ดังนั้น 2n-9 เป็นจำนวนเต็ม จึงต้องให้เศษเป็นจำนวนเต็มด้วย คือ 1007
นั่นคือเมื่อ 1007 หารด้วย 2n-9 ลงตัว แล้ว 3n^2 +66n -106 หารด้วย 2n-9 ลงตัว
1007 แยกตัวประกอบได้เป็น 1, 19, 53, 1007 หมายความว่า 2n-9 จะต้องมีค่าเป็นตัวใดตัวหนึ่งในนี้ --> n = 5, 14, 31, 508
จากทฤษฎีเศษเหลือ 3n^2 +66n -106 หารด้วย 3n-5 จะเหลือเศษ 37/3
นั่นคือเมื่อ 37 ต้องหารด้วย 3n-5 ลงตัวแล้ว 3n^2 +66n -106 หารด้วย 3n-5 ลงตัว
37 แยกตัวประกอบได้เป็น 1, 37 ดังนั้น 3n-5 = 1, 37
--> n = 2, 14
เมื่อนำไป intersect กับข้างต้นที่ว่า n = 5, 14, 31, 508
จะได้ n = 14
หมายความว่า เมื่อ n = 14 แล้ว 3n^2 +66n -106 หารลงตัวด้วย ทั้ง 2n-9 และ 3n-5
ค่อนข้างงง ๆ แต่ก็ไม่น่าผิด
จำนวนนับ n ที่ทำให้ m เป็นจำนวนเต็ม ได้แก่อะไรบ้างครับ???
