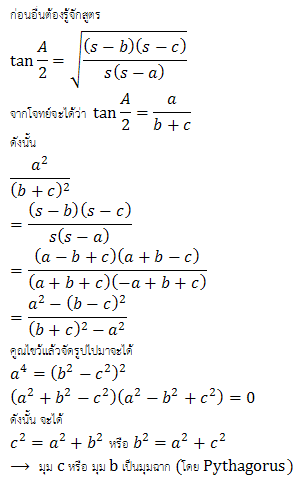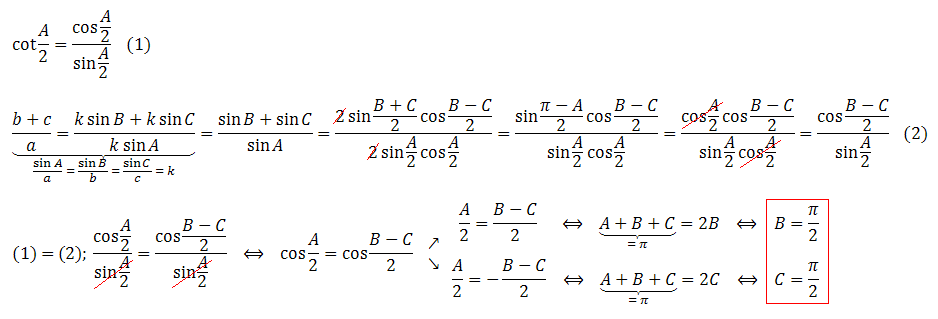ลองทำแบบเรขาคณิตดู
ก่อนอื่น ต้องพิสูจน์ง่าย ๆ ก่อนว่า b ไม่เท่ากับ c
เพราะถ้า b = c เมื่อเราลาก AH เส้นตั้งฉากกับ BC จะได้ว่า มุม BAH = A/2
ดังนั้นจากที่กำหนดว่า cot(A/2) = (b+c)/a = 2b/a เพราะกำหนดว่า b = c ด้วย
จะทำให้ ด้าน AH ยาวเท่ากับ b ซึ่งเป็นไปไม่ได้ เพราะด้าน AC ซึ่งเป็นด้านตรงข้ามมุมฉากของสามเหลี่ยม ACH ยาวเท่ากับ b อยู่แล้ว
ดังนั้น b ไม่เท่ากับ c
กำหนดให้ b > c
สร้างเพิ่มเติม โดยการลาก BA ออกไปถึงจุด X โดยที่ AX = AC แล้วลาก XC
จะได้ว่า มุม BXC = A/2 และด้าน BX ยาว b+c
จากจุด B ลาก BY ตั้งฉากกับ BX โดยที่ Y จะอยู่บนด้าน XC หรือส่วนต่อของ XC
จาก cot(A/2) = (b+c)/a จะได้ว่า BY = a
กรณีที่ 1: Y อยู่ตรง C พอดี จะได้มุม XBY =ABC และเป็นมุมฉาก
(กรณีที่ 2: Y อยู่ระหว่าง X กับ C และจาก BY = BC = a ดังนั้นมุม BYC = มุม BCY แต่มุม BYC = มุม XBY (90 องศา) + มุม BXY แสดงว่ามุม BYC เป็นมุมป้าน ทำให้ BCY เป็นมุมป้านด้วย ซึ่งเป็นไปไม่ได้ที่สามเหลี่ยม BYC จะมีมุมป้าน 2 มุม
กรณีที่ 3: Y อยู่บนส่วนต่อของ XC ก็จะได้เช่นเดิมว่า BY = BC = a และมุม BYC = มุม BCY แต่เนื่องจาก b > c ดังนั้น มุม ACB ต้องเป็นมุมแหลม ยังผลให้ มุม BCY เป็นมุมป้าน (มุม ACB + มุม BCY = 180 องศา) และทำให้มุม BYC เป็นมุมป้านด้วย ซึ่งเป็นไปไม่ได้ที่สามเหลี่ยม BYC จะมีมุมป้าน 2 มุม)
ขอแก้ไข กรณีที่ 2 และ 3 ที่อยู่ในวงเล็บ
กรณีที่ 2 และ 3; Y อยู่ระหว่าง X กับ C หรือ Y อยู่บนส่วนต่อของ XC จะได้เหมือนกันว่า BY = BC = a
ดังนั้นมุม BYC = มุม BCY = A/2 + C ยังผลให้ มุม BYX = A/2 + B (A, B และ C คือค่าของมุม BAC, ABC และ ACB ตามลำดับ)
ดังนั้น มุม BYX + มุม BXY = A/2 + A/2 + B = A + B
แต่ มุม BYX + มุม BXY = 180 - มุม XBY = 180 - 90 = 90
แสดงว่า A+B = 90 --> C = 90 แต่กำหนดแล้วว่า มุม B > มุม C (จาก b > c)
สรุปเป็นไปได้กรณีเดียวคือ กรณีที่ 1 คือมุม ABC เป็นมุมฉาก
ถ้าจะกำหนดให้ มุม c > b ก็พิสูจน์ในทำนองเดียวกัน แต่จะลากต่อ CA แทนที่จะลากต่อจากเส้น BA และจะได้ว่า มุม ACB เป็นมุมฉาก
อ่านแล้วคงงงมากเพราะไม่มีรูปประกอบ ใครก็ได้ช่วยวาดรูปให้ที จะขอบคุณมากครับ
แก้ไขเมื่อ 17 ก.ย. 55 21:44:42