ในปี ค.ศ. 1846 ที่ท่านเริ่มเรียนที่มหาวิทยาลัยแห่งเกอตติงเกนท่านเลือกเรียนวิชานิรุกติศาสตร์ และเทวศาสตร์ เป็นวิชาเอก แต่หลังจากได้ฟังปาฐกถาเกี่ยวกับทฤษฎีสมการ (Theory of Equations) และอินทิกรัลจำกัดเขต โดยสเตอร์น (Stern) และวิธีกำลังสองน้อยสุดโดยเกาส์ท่านประทับใจมากจึงเปลี่ยนมาเลือกคณิตศาสตร์เป็นวิชาเอก หลังจากเรียนที่เกอตติงเกน 1 ปี ท่านไปเรียนที่เบอร์ลิน เรียนกลศาสตร์และพีชคณิตชั้นสูงกับยาโคบี (Jocobi) เรียนทฤษฎีจำนวนและการวิเคราะห์กับดีริคเลต (Dirichlet) เรียนเราขาคณิตสมัยใหม่กับสไตเนอร์ (Steiner) และเรียนฟังก์ชันอิลิปติก (Elliptic function) จากไอเซนสไตน์ (Eisenstein) รีมันน์ใช้เวลาเรียนที่มหาวิทยาลัยแห่งเบอร์ลิน 2 ปี หลังจากนั้นท่านกลับไปที่เกอตติงเกน
ในเดือนกันยายน ปี ค.ศ. 1851 รีมันน์ส่งวิทยานิพนธ์สำหรับปริญญาเอกชื่อ Grundlagen fur eine allegemeine Theorie der Functionen einer veranderlichen complexen Grosse (รากฐานของทฤษฎีของฟังก์ชันตัวแปรเชิงซ้อน) ให้เกาส์พิจารณา เกาส์รายงานต่อคณะปรัชญาของมหาวิทยาลัยแห่งเกอตติงเกน ดังนี้
วิทยานิพนธ์ที่คุณรีมันน์เสนอมานั้น แสดงว่าผู้เสนอเจาะลึกถึงแก่นแท้ของเรื่องที่ตนศึกษาแสดงออกถึงความคิดริเริ่มสร้างสรรค์ทางคณิตศาสตร์อย่างแท้จริง วิทยานิพนธ์ฉบับบนี้ให้ความมุ่งหมายชัดแจ้งกระทัดรัดและบางแห่งสวยงามมาก ผู้อ่านส่วนใหญ่อาจต้องการให้ผู้เสนอจัดลำดับของเนื้อหาให้ชัดเจนกว่านี้ โดยส่วนรวมแล้ววิทยานิพนธ์ฉบับนี้มีทั้งสารและคุณค่าสูงส่งเกินมาตรฐานของวิทยานิพนธ์ระดับปริญญาเอก รีมันน์ได้เสนอมโนมติเกี่ยวกับพื้นผิวรีมันน์ (Riemann surface) ซึ่งเป็นการนำโทโพโลยีมาใช้ในวิชาการวิเคราะห์ นอกจากนั้นยังให้ความกระจ่างชัดเกี่ยวกับการอินทิเกรตได้ (integrability) โดยให้บทนิยามซึ่งปัจจุบันเราให้ชื่อว่าอินทิกรัลแบบรีมันน์ (Riemann interal)
หลังจากได้รับปริญญาเอกแล้วรีมันน์ใช้อีกสองปีครึ่งเตรียมตัวเพื่อได้เป็นผู้บรรยาย คณิตศาสตร์ ที่มหาวิทยาลัยแห่งเกอตติงเกน โดยปาฐกถาเรื่อง Uber die Hypothesen, Welche der Geometric zu Gunde liegen (สัจพจน์ซึ่งเป็นรากฐานของเรขาคณิต) ในปี ค.ศ. 1854 รีมันน์ได้แสดงถึงข้อแตกต่าง
ระหว่างการต่อไปเรื่อยๆ (unboundedness) และความยาวไม่จำกัด (infinite extent)
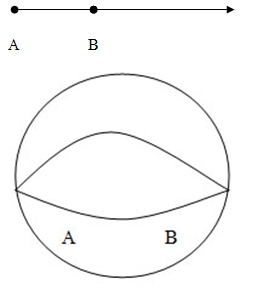
ในระนาบปกติจากส่วนของเส้นตรง AB เราสามารถลากต่อจาก B ไปเรื่อยๆ และส่วนที่ต่อออกไปจะมีความยาวไม่จำกัด
บนพื้นผิวทรงกลม จากส่วนของเส้น AB เราสามารถลากต่อจาก B ไปเรื่อย ๆ แต่ส่วนที่ต่อออกไปจะมีความยาวจำกัด








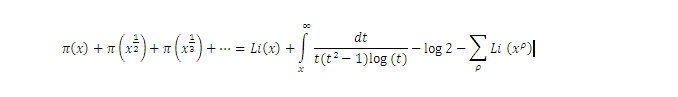






 ... เข้ามาดู
... เข้ามาดู