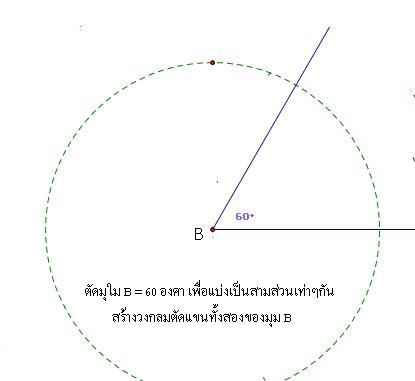
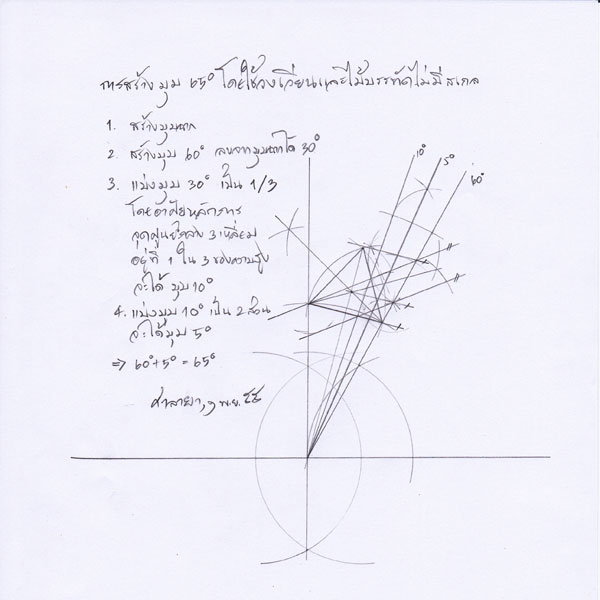
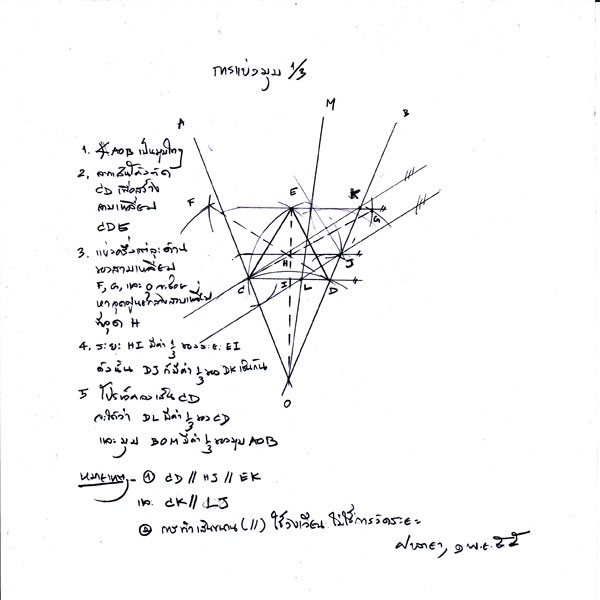
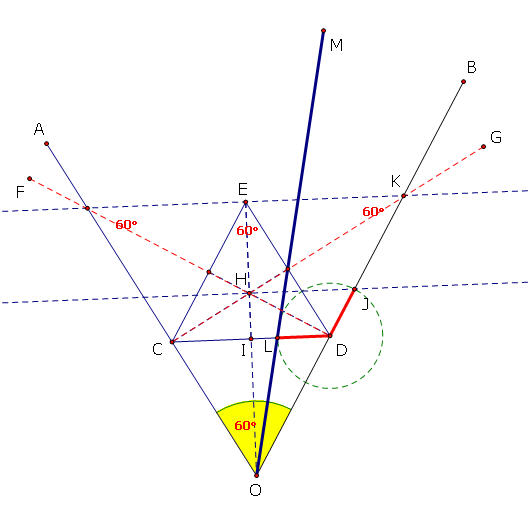
สวัสดีครับ
เราไม่สามารถสร้างมุม 65 องศา ด้วยสันตรงกับวงเวียนได้ครับ
เราจะสามารถสร้างมุมที่เป็นจำนวนนับด้วยสันตรงกับวงเวียนได้ ก็ต่อเมื่อ มุมนั้น (เป็นองศา) หารด้วย 3 ลงตัวครับ เนื่องจาก 65 หารด้วย 3 ไม่ลงตัว มุม 65 องศาก็สร้างไม่ได้ครับ
ทำไมถึงต้องหารด้วย 3 ลงตัว ?
ก่อนอื่นจะสมมติว่ามุม 60 สร้างได้ และ มุม 72 สร้างได้ (มุม 60 สร้างจากสามเหลี่ยมด้านเท่า มุม 72 สร้างจากห้าเหล่ียมด้านเท่า ดูตัวอย่างได้ที่ http://www.mathopenref.com/constinpentagon.html)
และจะอ้างทฤษฎีที่ว่ามุม 20 สร้างไม่ได้ (ต้องใช้ความรู้ abstract algebra ถ้ายังไงผมจะพูดคร่าวๆ ในตอนท้ายครับ)
เนื่องจากเราสร้างมุม 60 กับ 72 ได้ เราก็สามารถสร้างผลต่างของมุมได้ 72-60 = 12 ดังนั้นเราสร้างมุม 12 องศาได้ เนื่องจากเราแบ่งครึ่งมุมด้วยสันตรงกับวงเวียนได้ เราจึงสร้างมุม 12/4 = 3 องศาได้
ดังนั้นมุมใดๆ ก็ตามที่หารด้วย 3 ลงตัว ก็สามารถสร้างได้ด้วยการ copy มุม 3 องศาไปเรื่อยๆ
ต่อไปจะแสดงว่ามุม 1 องศา สร้างไม่ได้
ถ้ามุม 1 องศาสร้างได้ เราสามารถสร้างมุม 20 องศา ด้วยการสร้างมุม 3 องศา 7 ครั้ง แล้วลบออกด้วยมุม 1 องศา 3*7-1 = 20. ดังนั้นเราจะสร้างมุม 20 องศาได้
แต่เรารู้ว่ามุม 20 องศาไม่ได้ ดังนั้นมุม 1 องศาจึงสร้างไม่ได้
ต่อไปจะแสดงว่ามุมที่หารด้วย 3 ไม่ลงตัว สร้างไม่ได้
สมมติว่ามุม n หารด้วย 3 ไม่ลงตัว เราเอา n ไปหารด้วย 3 จะได้ 1 หรือ 2
สมมติว่าได้ 1 เราเขียนได้ว่า n = 3k + 1
ถ้าเราสร้าง n ได้ เราก็สามารถสร้างมุม 1 องศาได้ โดยเอามุม 3k มาลบออก
แต่เราสร้างมุม 1 องศาไม่ได้
อีกกรณีคือ n = 3k+2 นั่นคือ n = 3k + 3-1 = 3(k+1) - 1
ถ้าเราสร้างมุม n องศาได้ เราจะสามารถสร้างมุม 1 องศาได้ โดยเอามุม 3(k+1) มาลบออก แต่เราสร้างมุม 1 องศาไม่ได้
ดังนั้นเราจึงสร้างมุม n องศาไม่ได้ครับ ถ้า n หารด้วย 3 ไม่ลงตัว
เนื่องจาก 65 หารด้วย 3 ไม่ลงตัว ก็สร้างไม่ได้ครับ
ปล. ความจริงจะถ้ายอมรับว่ามุม 20 องศาสร้างไม่ได้ เราก็สามารถอ้างได้ว่า มุม 65 สร้างไม่ได้ เพราะถ้าสร้างได้ เราจะมาสามารถสร้างมุม 20 องศาได้จากการเอามุม 45 ไปหักออกจากมุม 65 ครับ แต่ข้อความข้างบน general กว่า
====How do you draw a 65 degree angle with compass?===
