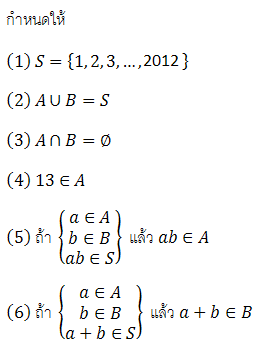ความคิดเห็นที่ 1 คิดได้เท่ากันกับ จขกท. ครับ จากคุณ : เทส เขียนเมื่อ : 17 พ.ย. 55 00:50:37 A:27.55.5.92 X: TicketID:378274

ความคิดเห็นที่ 2 เซต A B สอดคล้องกับเงื่อนไขทั้งหกข้อใช่ไหมคะ ถ้าใช่เราว่า A=S นะ จากคุณ : moonoinee เขียนเมื่อ : 17 พ.ย. 55 08:08:53

ความคิดเห็นที่ 3 ขอลองนะคับ ไม่แน่ใจถูกรึเปล่า ตอนนี้ได้แค่นี้น่ะคับ ขอตัดกรณี B เป็นเซตว่างออกไปนะคับ (จะได้ A=S และยังสอดคล้องเงื่อนไขทุกข้อ) Claim: 1,2,...,12ฮB - ถ้า 1ฮA เนื่องจาก B ไม่เป็นเซตว่าง จึงได้ว่าต้องมี nฮB แต่ n = 1ดnฮA เกิดข้อขัดแย้ง ดังนั้น 1ฮB - ถ้า 2ฮA จะได้ว่า 3=2+1ฮB และ 5=2+3ฮB และ 10=2ด5ฮA และ 13=10+3ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 2ฮB - ถ้า 3ฮA จะได้ว่า 6=3ด2ฮA และ 12=6ด2ฮA และ 13=12+1ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 3ฮB - ถ้า 4ฮA จะได้ว่า 12=4ด3ฮA และ 13=12+1ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 4ฮB - ถ้า 5ฮA จะได้ว่า 8=5+3ฮB และ 13=5+8ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 5ฮB - ถ้า 6ฮA จะได้ว่า 12=6ด2ฮA และ 13=12+1ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 6ฮB - ถ้า 7ฮA จะได้ว่า 13=7+6ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 7ฮB - ถ้า 8ฮA จะได้ว่า 13=8+5ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 8ฮB - ถ้า 9ฮA จะได้ว่า 13=9+4ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 9ฮB - ถ้า 10ฮA จะได้ว่า 13=10+3ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 10ฮB - ถ้า 11ฮA จะได้ว่า 13=11+2ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 11ฮB - ถ้า 12ฮA จะได้ว่า 13=12+1ฮB แต่ 13ฮA เกิดข้อขัดแย้ง ดังนั้น 12ฮB เราจึงได้ว่าขณะนี้ 13ฮA และ 1,2,...,12ฮB ทำให้ได้ว่า จำนวนที่อยู่ใน A อย่างน้อยๆ จะต้องหารด้วย 13 ลงตัว (มาจากการคูณด้วย 13) แก้ไขเมื่อ 17 พ.ย. 55 08:19:36 จากคุณ : ชโรนนท์ เขียนเมื่อ : 17 พ.ย. 55 08:18:40

ความคิดเห็นที่ 4 ทีนี้สังเกตว่า 14 = 13+1, 15 = 13+2 ,..., 25 = 13+12 และ 26 = 13ด2 ดังนั้น 14,15,...,25ฮB และ 26ฮA จึงเห็นได้ว่าบรรดาจำนวนที่ 13 หารลงตัวจะต้องอยู่ใน A ที่เหลือจะอยู่ใน B จนถึงเลข 168 แต่ถ้าเราไล่มาเรื่อยๆ จนถึง 169 = 13ด13 ล่ะ? เราใช้เหตุผลเดียวกันกับเมื่อกี้ไม่ได้ เพราะ 13ฯB อย่างไรก็ตาม ถ้า 169ฮB จะได้ว่า 182 = 13+169ฮB แต่ 182 = 13ด14ฮA เกิดข้อขัดแย้ง ดังนั้น 169ฮA ซึ่งทำให้ 170 = 169+1ฮB, 171 = 169+2ฮB,...,182 = 13ด14ฮA เช่นเดิม และเนื่องจาก 13ด13ด13>2012 เราจึงมั่นใจได้ว่าจำนวนที่หารด้วย 13 ลงตัวต้องอยู่ใน A เท่านั้น นั่นคือ A = {13,26,39,...,2002} ซึ่งมีจำนวนสมาชิก 154 จำนวน จากคุณ : ชโรนนท์ เขียนเมื่อ : 17 พ.ย. 55 08:36:22

ความคิดเห็นที่ 5 หรอครับ ผมขอถาม 2011 อยุ่ใน เอ 1 อยุใน บี 2011 คุน 1 อยุใน เอ 2011 บวก 1 อยุ่ใน บี ทำไมคุณชโรนนท์ไม่เอา 2011 เข้าด้วยหละครับ ?? ผมเชคเงื่อนไขผิดหรือเปล่าครับ จากคุณ : เทส เขียนเมื่อ : 17 พ.ย. 55 12:22:20 A:27.55.12.229 X: TicketID:378274

ความคิดเห็นที่ 6 คุณเทส 2011 อยู่ในB ครับ ไม่ได้อยู่ใน A ---------------------------------------------------------------------------------------- ถ้าไม่มีอะไรผิดพลาดผมคิดว่าคำตอบทั้งหมดที่สอดคล้องมีดังนี้ครับ 1. A = S และ B เป็นเซตว่าง 2. A = {x| 0 < x < 2013 และ13หารxลงตัว } และ  B = {x| 0 < x < 2013 และ13หารxไม่ลงตัวลงตัว } และไม่มีคำตอบอื่นนอกจากนี้อีกแล้ว ซึ่งการพิสูจน์ค่อนข้างจุกจิกมากขอละเอาไว้ก่อนนะครับ หมายเหตุ : ตัวแปรที่ใช้แทนจำนวนทุกตัวถือเป็นจำนวนเต็ม แก้ไข : คำตอบที่3ตัดทิ้งใช้ไม่ได้ แก้ไขเมื่อ 17 พ.ย. 55 14:19:41 แก้ไขเมื่อ 17 พ.ย. 55 13:56:52 จากคุณ : อิอิคุง เขียนเมื่อ : 17 พ.ย. 55 13:52:13

ความคิดเห็นที่ 7 คุณอิอิ ผมก็กังถามว่าทำไมเอา 2011 เข้าเอไม่ได้ยังไงล่ะครับ จากคุณ : เทส เขียนเมื่อ : 17 พ.ย. 55 17:46:40 A:27.55.15.195 X: TicketID:378274

ความคิดเห็นที่ 8 ^ เพราะ A ต้องเป็นเซต{1,2,...2012} หรือไม่ก็เซตของจำนวนที่หารด้วย13ลงตัว อย่างใดอย่างหนึ่งเท่านั้นจึงจะตรงกับเงื่อนไขที่โจทย์กำหนด แต่คุณชโรนนท์สนใจเฉพาะคำตอบที่Bไม่เป็นเซตว่างจึงตัดกรณีที่Bเป็นเซตว่างออกไป ทำให้ A ต้องเป็นเซตของจำนวนที่หารด้วย13ลงตัวเท่านั้น ซึ่ง 2011หารด้วย13ไม่ลงตัว  2011จึงไม่สามารถเป็นสมาชิกของเซตAได้ครับ แก้ไขเมื่อ 17 พ.ย. 55 20:00:15 แก้ไขเมื่อ 17 พ.ย. 55 19:59:36 จากคุณ : อิอิคุง เขียนเมื่อ : 17 พ.ย. 55 19:56:21

ความคิดเห็นที่ 9 โจทย์กำหนดแค่ 13 เป็นสมาชิกของ a ครับ ไม่/ด้กำหนดว่า a ต้องหาร 13 ลงตัว และ บีของผมที่เป็น 1 ก้อไม่ได้บอกว่า บีเป็นเซตว่าง จากคุณ : เทส เขียนเมื่อ : 17 พ.ย. 55 20:20:01 A:27.55.15.206 X: TicketID:378274

ความคิดเห็นที่ 10 คณอธิบาย แบบเอาผลมาอธิบายเหตุแบบนี้ไม่ได้ครับ เพราะผมกำลังสงสัย คำตอบของคุณชโรนนท์อยู่ ผมรอให้คุณชโรนนมาชี้แจงดีกว่า งง จากคุณ : เทส เขียนเมื่อ : 17 พ.ย. 55 20:21:52 A:27.55.15.206 X: TicketID:378274

ความคิดเห็นที่ 11 โจทย์กำหนดแค่ 13 เป็นสมาชิกของ a ครับ ไม่/ด้กำหนดว่า a ต้องหาร 13 ลงตัว --------------------------------------------------------- โจทย์ไม่ได้บอกว่าสมาชิกในเซต A ต้องหารด้วย 13 ลงตัว ก็จริง แต่จากสิ่งที่โจทย์บอกมาทั้งหมดทำให้เราพิสูจน์ได้ว่าถ้าBไม่เป็นเซตว่างแล้ว ทุกสมาชิกในเซต A ต้องหาร 13 ลงตัว เท่านั้นครับ สรุปคุณเทสกำลังสงสัยว่า ทำไม "ถ้าBไม่เป็นเซตว่างแล้ว ทุกสมาชิกในเซต A ต้องหาร 13 ลงตัว เท่านั้น" ใช่หรือเปล่า? จากคุณ : อิอิคุง เขียนเมื่อ : 17 พ.ย. 55 20:37:47

ความคิดเห็นที่ 12 เรียนถามทุกท่านครับ จากประโยคนี้... " The set S = {1,2,3, . . . ,2012} is partitioned into two disjoint subsets A and B ... " A และ B สามารถเป็นเซตว่างได้มั้ยครับ? ป.ล. ส่วนตัวได้คำตอบเท่ากับ คุณ ชโรนนท์ ในกรณีที่ B ไม่เป็นเซตว่างครับ วิธีคิดก็ทำนองเดียวกันครับ แก้ไขเมื่อ 17 พ.ย. 55 22:09:37 จากคุณ : TIYHz เขียนเมื่อ : 17 พ.ย. 55 21:50:18

ความคิดเห็นที่ 13 ถ้าแบบนี้เข้าใจว่า A และ B เป็นเซตว่างไม่ได้ครับ จากคุณ : อิอิคุง เขียนเมื่อ : 17 พ.ย. 55 22:07:03

ความคิดเห็นที่ 14 ตามนี้คับ จากคุณ : ชโรนนท์ เขียนเมื่อ : 17 พ.ย. 55 22:13:38

ความคิดเห็นที่ 15 คุณต้องพิสุจน์ว่า ผมเอา 2011 เข้า เอ แทนที่จะอยุ่ใน บี แล้วขัดแย้งกับเงื่อนไขโจทตรงไหนต่างหากละครับ ถ้าหาไม่ได้ก้อแปลว่า ข้อสรุป 13 หารลงยังไม่ใช่ ข้อสรุปที่ถุกไงล่ะค้าบ 55555 เพราะผมดูแล้วมันก้อไม่ได้ขัดกับสิ่งที่โจทย์ให้เลย แทนได้ทุกเงื่อนไขครับ ขอบคุณครับ จากคุณ : เทส เขียนเมื่อ : 18 พ.ย. 55 01:39:45 A:27.55.15.206 X: TicketID:378274

ความคิดเห็นที่ 16 มันมีเรื่องตลกตรงที่ สมมุติ คำถาม อะไรบินได้ คุณบอก หมาบินได้ ผมบอก นกก็บินได้ คุณดันมาบอก ผมผิด เพราะ นกไม่ใช่หมา !!! อ้าว ผมต้องสนโจทสิครับ โจทไม่ได้บอกว่าหมา แล้วผมก้อเข้าเงื่อนไข 555555555555 คุณต้องบอกว่า ที่คุณคิดว่านกผมบินไม่ได้ มันขัดเงื่อนโจทยังไงไม่ใช่หรอออออ จากคุณ : เทส เขียนเมื่อ : 18 พ.ย. 55 01:46:08 A:27.55.15.206 X: TicketID:378274

ความคิดเห็นที่ 17 เรียนตามตรงตอนแรกผมอ่านความเห็น5ของคุณเทสแล้วไม่ค่อยเข้าใจคำถาม เพราะในความเห็น5คุณไม่ได้ขึ้นต้นข้อความด้วยคำว่า “ถ้า”หรือ “สมมติ” และไม่ได้ลงท้ายข้อความด้วยประโยคที่มีความหมายทำนองว่า “ก็ไม่ได้ขัดกับเงื่อนไขของโจทย์แต่อย่างใด” จึงทำให้ผมเข้าใจคำถามของคุณผิดไปจากที่คุณตั้งใจจะสื่อ แต่พออ่าน2ความเห็นสุดท้ายประกอบ   ตอนนี้ผมเข้าใจสิ่งที่คุณเทสต้องการแล้ว      ก็ขออธิบายอย่างนี้ครับ 1. จากความเห็น3ของคุณชโรนนท์ได้อธิบายแล้วว่า9ต้องอยู่ใน B 2. เนื่องจาก 13อยู่ในA และ 9อยู่ในB และ 13+9 = 22 อยู่ในS ดังนั้น 22 ต้องอยู่ในB (ถ้า22อยู่ในAจะขัดกับเงื่อนไข(6)ของโจทย์) 3. เนื่องจาก 13อยู่ในA และ 22อยู่ในB และ 13+22 = 35 อยู่ในS ดังนั้น 35 ต้องอยู่ในB (ถ้า35อยู่ในAจะขัดกับเงื่อนไข(6)ของโจทย์) 4. เนื่องจาก 13อยู่ในA และ 35อยู่ในB และ 13+35 = 48 อยู่ในS ดังนั้น 48 ต้องอยู่ในB (ถ้า48อยู่ในAจะขัดกับเงื่อนไข(6)ของโจทย์)         ...............         ...............         ............... 155. เนื่องจาก 13อยู่ในA และ 1998อยู่ในB และ 13+1998 = 2011 อยู่ในS ดังนั้น 2011 ต้องอยู่ในB(ถ้า2011อยู่ในAจะขัดกับเงื่อนไข(6)ของโจทย์) ถ้าให้สรุปสั้นๆก็คือ เนื่องจาก13อยู่ในAและ9อยู่ในB  โดยเงื่อนไข(6)ของโจทย์จะได้ว่า จำนวนที่สามารถเขียนในรูป13k+9  (ซึ่งก็คือจำนวนที่หารด้วย13แล้วเหลือเศษ9) ทุกตัวที่อยู่ในS ต้องอยู่ในB ซึ่ง2011 สามารถเขียนได้ในรูป13k+9 (k=154) จึงต้องอยู่ในBครับ จากคุณ : อิอิคุง เขียนเมื่อ : 18 พ.ย. 55 07:14:49

ความคิดเห็นที่ 18 เพื่อให้คุณเทสมั่นใจว่าAคือเซตของจำนวนที่13หารลงตัว ผมคงต้องพิสูจน์ให้เป็นเรื่องเป็นราว 1. อาศัยอานิสงค์จากความเห็น3ซึ่งได้พิสูจน์แล้วว่า 1,2,…,12 อยู่ใน B  และเนื่องจาก 13อยู่ในA  โดยเงื่อนไขข้อ(6)ของโจทย์จะได้ว่า     จำนวนที่สามารถเขียนในรูป 13k+1 , 13k+2 ,…, 13k+12 (ซึ่งก็คือจำนวนที่13หารไม่ลงตัว) ทุกตัวที่อยู่ใน S ต้องอยู่ในB 2. เนื่องจาก13อยู่ในA และ จำนวนที่สามารถเขียนในรูป 13k+1 , 13k+2 ,…, 13k+12 (ซึ่งก็คือจำนวนที่13หารไม่ลงตัว) ทุกตัวที่อยู่ใน S ต้องอยู่ในB        โดยเงื่อนไขข้อ(5)ของโจทย์จะได้ว่า จำนวนที่สามารถเขียนในรูป 13(13k+1), 13(13k+2) , … , 13(13k+12) ทุกตัวที่อยู่ในS ต้องอยู่ในA 3. พิจารณาจำนวนที่เขียนได้ในรูป 13(13k) = 169k        สมมติว่ามีจำนวนที่เขียนได้ในรูป 169k ที่อยู่ในSบางตัวอยู่ในB จะได้ว่า 1 <= k <= 11  และจะได้ว่า  1< 169k+13 < 2012 นั่นคือ 169k+13 อยู่ในS      ตอนนี้เรามี 169kอยู่ในBจากการสมมติ , 13อยู่ในA , 169k+13อยู่ในS  โดยเงื่อนไข(6)ของโจทย์ ทำให้ได้ว่า 169k+13 = 13(13k+1) ต้องอยู่ในB        แต่จากข้อ2 ทุกจำนวนที่สามารถเขียนในรูป 13(13k+1) ที่อยู่ในSไปอยู่ในAหมดแล้วจึงเกิดข้อขัดแย้ง        ดังนั้นทุกจำนวนที่เขียนได้ในรูป13(13k)ที่อยู่ในS ต้องอยู่ในA 4. จากข้อ2และ3เราได้ว่า จำนวนที่เขียนได้ในรูป 13(13k), 13(13k+1), 13(13k+2) , … , 13(13k+12) ทุกตัวที่อยู่ในS ต้องอยู่ในA        นั่นคือทุกจำนวนที่ 13หารลงตัวที่อยู่ในSต้องอยู่ในA 5. จากข้อ4เราได้ {x| 0 < x < 2013 และ13หารxลงตัว } อ A และจากข้อ1เราได้ {x| 0 < x < 2013 และ13หารxไม่ลงตัว } อ B 6. สมมติถ้า x อยู่ในA และสมมติว่า x ไม่อยู่ใน {x| 0 < x < 2013 และ13หารxลงตัว }   จะได้ว่า x อยู่ใน {x| 0 < x < 2013 และ13หารxไม่ลงตัว }      ซึ่งจะได้ x อยู่ใน B  เกิดข้อขัดแย้งกับที่ว่า x อยู่ใน A   ดังนั้น ถ้า x อยู่ใน A แล้ว x ต้องอยู่ใน {x| 0 < x < 2013 และ13หารxลงตัว }      นั่นคือ A อ {x| 0 < x < 2013 และ13หารxลงตัว }   และทำในทำนองเดียวกันเราจะได้  B อ {x| 0 < x < 2013 และ13หารxไม่ลงตัว } 7. จากข้อ5และ6สรุปได้ว่า A = {x| 0 < x < 2013 และ13หารxลงตัว } และ B = {x| 0 < x < 2013 และ13หารxไม่ลงตัว } จากคุณ : อิอิคุง เขียนเมื่อ : 18 พ.ย. 55 07:32:40

ความคิดเห็นที่ 19 ผมชอบโจทย์ข้อนี้ครับ เด๋วผมจะเอาประเด็นนี้ไปตั้งกระทู้ใหม่ จากคุณ : เทส เขียนเมื่อ : 18 พ.ย. 55 07:43:51 A:27.55.7.152 X: TicketID:378274

ความคิดเห็นที่ 20 มีเรื่องคาใจนิดหน่อย จากคุณ : เทส เขียนเมื่อ : 18 พ.ย. 55 07:51:23 A:27.55.7.152 X: TicketID:378274

ความคิดเห็นที่ 21 ขอบคุนๆอิอิคุงครับ จากคุณ : เทส เขียนเมื่อ : 18 พ.ย. 55 16:40:34 A:27.55.15.228 X: TicketID:378274